Гидравлика 4 страница

- хорошие электроизоляционные свойства. Отсутствие солей, которые способствуют образованию гальванических пар;

- неизменность свойств с течением времени, отсутствие выпадения осадков, окисления;

- достаточно высокая пожаробезопасносгь, характеризующаяся температурой вспышки;

- малая токсичность жидкости и ее паров при работе с ней людей;

- достаточно низкая стоимость.

Для надежной и длительной работы гидропривода основным требованием к рабочим жидкостям является способность сохранять длительное время свои эксплуатационные качества (физические свойства и химический состав). Кроме того, рабочие жидкости должны обладать антикоррозийными и смазывающими свойствами, т.е. не только не вызывать коррозию, но и обеспечивать эффективное смазывание трущихся поверхностей, образуя на них прочный слой, который исключит полностью или частично контакт этих поверхностей между собой и уменьшит их износ.

Вредное влияние на работу гидропривода оказывают пузырьки нерастворенного воздуха, поэтому рабочие жидкости должны легко выделять эти пузырьки без образования пены на поверхности жидкости в гидробаках. Жидкости должны иметь достаточно высокую температуру кипения, мало испаряться при работе, а их пары не должны быть вредными для здоровья людей, взрыво- и пожароопасными при работе оборудования.

В качестве рабочих жидкостей для гидроприводов используют в основном минеральные масла, получаемые путем перегонки нефти. Эти масла являются основой в которую добавляют антипенные, антиокислительные и другие присадки, повышающие эксплуатационные качества масел. В гидроприводах машин, работающих при повышенных или отрицательных температурах окружающего воздуха, повышенной взрывоопасности и других особых условиях, в качестве рабочих жидкостей применяют синтетические жидкости или эмульсии на водной основе. Однако по сравнению с минеральными маслами синтетические жидкости значительно дороже в изготовлении, а водно-эмульсионные жидкости уступают маслам по антикоррозийным и смазывающим свойствам.

3. ОСНОВЫ КИНЕМАТИКИ СПЛОШНЫХ СРЕД

3.1. Два метода описания движения жидкостей и газов

В механике существуют два метода изучения движения. Первый метод - метод Лагранжа - заключается в том, что движение частицы изучается наблюдателем, движущимся с этой частицей. В этом случае движение задается положением частиц в функции от времени и от их начальных координат 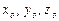в некоторый момент времени 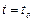, т.е.

;

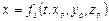; (3.1)

.

Задача сводится к определению траектории движения частицы.

Второй метод - метод Эйлера - заключается в том, что движение среды изучается наблюдателем, расположенным в неподвижной точке. В этом случае движение среды определяется скоростями частиц в зависимости от времени 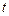и координат точек пространства х, у и z, относительно которых происходит движение, т.е.

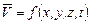(3.2)

или в проекциях

;

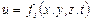; (3.3)

.

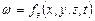Метод Лагранжа используется в гидродинамике редко, так как определять траектории обычно довольно сложных движений очень трудно. В основном пользуются методом Эйлера.

3.2. Понятие о линиях и трубках тока. Ускорение

жидкой частицы

Часть механики жидкостей и газов, в которой рассматриваются общие свойства движения без выяснения причин его возникновения, называется кинематикой. В кинематике изучается положение частиц жидкости в пространстве в зависимости от времени.

В отличие от теоретической механики, в которой изучается движение абсолютно твердого тела, а также движение отдельной точки или системы точек с фиксированным расстоянием между ними, в кинематике сплошных сред изучается движение деформируемых тел. В процессе движения таких тел изменяется первоначальная их форма и расстояние между двумя любыми частицами. Деформируемость является главной кинематической особенностью сплошных сред вообще и жидкостей и газов в частности.

Рассматриваемые здесь понятия и законы кинематики относятся не только к жидкостям и газам, но и ко всем сплошным или деформируемым средам. Таким образом, кинематика сплошных сред изучает геометрию движения жидких, газообразных и деформируемых твердых тел, имеющих одно общее свойство - сплошность или непрерывность среды.

Будем считать, что все кинематические величины непрерывны в пространстве и времени и дифференцируемы. В отдельных случаях непрерывность некоторых величин может нарушаться, могут появляться поверхности разрыва таких величин, как скорость, ускорение и пр.

Движение сплошных сред характеризуется, прежде всего, скоростями ее частиц. В каждый момент времени каждая частица имеет определенную по величине и по направлению скорость. Картина скоростей в данный момент времени называется полем скоростей.

Если поле скоростей остается неизменным во времени, то движение называется стационарным, или установившимся. Если же оно зависит от времени, то движение будет нестационарным. В некоторых случаях характер движения будет зависеть от выбора системы координат. Так, в координатной системе, связанной с телом, движущимся с постоянной скоростью, обтекание этого тела (поезд, автомобиль и пр.) будет стационарным, в то время, как в неподвижной координатной системе (для неподвижного наблюдателя) движение среды, обтекающей тело, будет нестационарным.

В практике часто пользуются понятиями средних скоростей. Обычно усреднение скорости производится либо по времени, либо по площади некоторого сечения потока.

Среднее значение величины скорости за промежуток времени 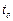представляет собой интеграл в виде

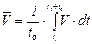. (3.4)

Средняя величина скорости по некоторой площади s определяется следующим образом:

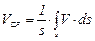. (3.5)

Вектор ускорения жидкой частицы, движущейся со скоростью V, является индивидуальной производной по времени от вектора скорости, т.е.

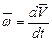. (3.6)

Так как вектор скорости в общем случае зависит от времени и координат, т.е.

, (3.7)

то по правилу дифференцирования сложной функции найдем

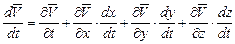, (3.8)

но производные от координат движущейся точки по времени есть соответствующие проекции скоростей, т.е.

. (3.9)

Тогда получим

. (3.10)

Первое слагаемое правой части равенства выражает изменение скорости во времени в некоторой фиксированной точке пространства, т.е, местное изменение, и поэтому называется локальной составляющей ускорения. Остальная часть ускорения характеризует изменение скорости частицы при ее перемещении и называется конвективной составляющей ускорения.

В проекциях на оси координат х, у и z уравнение (3.10) будет иметь вид

;

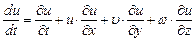; (3.11)

.

При изучении векторных полей, встречающихся в механике сплошных сред, пользуются некоторыми характерными линиями и поверхностями. Прежде чем перейти к их определению, рассмотрим некоторые общие понятия, относящиеся к любым векторным полям.

Векторной линией в поле векторов называется линия, в каждой точке которой в данный момент времени вектор касателен к ней. Совокупность векторных линий, проходящих через все точки некоторого контура, образуют векторную поверхность. Если контур, через все точки которого проходят векторные линии, замкнутый, то часть пространства, заключенная внутри векторной поверхности, образует векторную трубку.

Исходя из определения векторной линии, нетрудно получить ее уравнение. Так как в каждой точке контура (рис. 3.1) вектор а касателен к контуру, то, следовательно, вектор а и элементарный вектор dr совпадают по направлению и их векторное произведение равно нулю

.

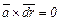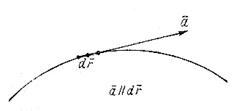
Рис. 3.1. Векторная линия

Из условия равенства нулю проекций этого векторного произведения следует, что

. (3.12)

Приведенные понятия можно применить к любым векторным полям. Применительно к наиболее распространенному в механике сплошных сред и гидромеханике векторному полю - полю скоростей - векторная линия называется линией тока, а векторная трубка - трубкой тока (рис. 3.2).

Рис. 3.2. Трубка тока

Очевидно, уравнение линии тока будет

. (3.13)

Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. При стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.

В любой точке трубки тока, т.е. боковой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу. Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток. Потоки конечных, размеров будем сначала рассматривать как совокупности элементарных струек, т.е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут скользить одна по, другой, но не будут перемешиваться одна с другой. Таким образом, элементарная струйка обладает тремя свойствами:

- форма элементарной струйки со временем не изменяется;

- скорости и давления в поперечных сечениях элементарной струйки есть величины постоянные;

- боковая поверхность элементарной струйки не проницаема.

Так как трубка тока образована совокупностью линий тока, то очевидно, что количество вещества, протекающего в любом сечении трубки, будет одним и тем же. Это означает, что в местах сужения трубки скорость движения несжимаемой жидкости увеличивается, а в местах расширения трубки она уменьшается.

Если рассматривать движение жидкой частицы во времени, то линия, по которой двигалась частица в некоторый промежуток времени, называется траекторией. Для стационарного движения линия тока и траектория совпадают, при нестационарном движении они отличаются друг от друга.

Как следует из определения, линия тока есть линия, в каждой точке которой нормальная составляющая скорости равна нулю, т.е. через линию тока нет перетекания. Таким образом, между двумя произвольными линиями тока количество протекающей жидкости постоянно. Поэтому для несжимаемой жидкости в местах, где линии тока сближаются, величина скорости увеличивается и, наоборот, там, где они расходятся, скорости убывают. Следовательно, любая твердая непроницаемая стенка обтекаемого тела (рис. 3.3) будет также линией тока.

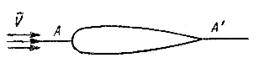
Рис. 3.3. Непроницаемая стенка обтекаемого тела

В общем случае через любую точку движущей среды в данный момент времени можно провести лишь одну линию тока, но существуют некоторые особые точки, в которых это правило нарушается. В особых точках линии тока пересекаются, следовательно, в этих точках вектор скорости должен иметь разные направления, что при конечном значении скорости невозможно. Поэтому в особых точках величина скорости должна быть равна либо нулю, либо бесконечности.

При обтекании тела так называемая нулевая линия тока, образующая непроницаемый контур тела, в точках А и А' (рис. 3.3) имеет особые точки. В этих точках, называемых критическими, величина скорости равна нулю.

Особая точка другого типа получается при рассмотрении задачи о вытекании среды из одной точки или, наоборот, при ее втекании в точку (рис. 3.4).

Рис. 3.4. Схема источников и стоков

Первое движение будем называть точечным источником, а второе - стоком. В обоих случаях в точках пересечения линий тока величина скорости обращается в бесконечность.

3.3. Расход элементарной струйки и расход

через поверхность

Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Под живым сечением, или просто сечением потока, понимают в общем случае поверхность в пределах потока, проведенную нормально к линиям тока.

Это количество можно измерить в единицах объема, в весовых единицах или в единицах массы, в связи с чем различают объемный Q, весовой и массовый 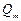расходы. Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость V одинаковой во всех точках каждого сечения. Следовательно, для этой струйки объемный (), весовой () и массовый () расходы будут равны:

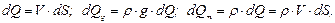(3.14)

где dS - площадь сечения струйки.

Основываясь на законе сохранения вещества, на предположении о сплошности (неразрывности) течения и на указанном выше свойстве трубки тока, заключающемся в ее «непроницаемости», для установившегося течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же:

(вдоль струйки). (3.15)

Это уравнение называется уравнением объемного расхода для элементарной струйки.

Рассмотрим понятие о потоке вектора скорости. В векторном анализе потоком любого вектора а называется интеграл по некоторой поверхности 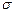от проекции вектора а на нормаль n в каждой точке поверхности, т.е.

. (3.16)

Соответственно с этим поток вектора скорости определяется величиной, равной

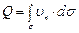. (3.17)

Поток вектора скорости физически представляет собой объемный расход некоторой жидкости (среды) через поверхность .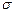

Если поверхность 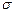замкнутая, то при отсутствии внутри поверхности источников и стоков поток вектора скорости через замкнутую поверхность будет равен нулю

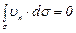. (3.18)

Для потока конечных размеров скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарных расходов струек, т.е.

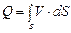. (3.19)

Обычно в рассмотрение вводят среднюю по сечению скорость 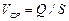, откуда в соответствии с выражениями (3.17) - (3.19) получаем

(вдоль потока). (3.20)

Аналогично уравнению (3.15) можно составить уравнение и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате будем иметь:

(вдоль потока). (3.21)

Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений. Уравнение расхода является следствием общего закона сохранения вещества для частных условий, в частности для условий сплошности (неразрывности) течения.

При наличии источника поток вектора скорости будет составлять

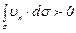, (3.22)

а при наличии стока

. (3.23)

3.4. Уравнение неразрывности (сплошности)

На движение сплошных сред распространяются общие законы природы. Среди этих законов особенно важное и наиболее общее значение имеют законы сохранения. В механике обычно рассматриваются законы сохранения четырех величин: массы, количества движения, момента количества движения и энергии. Все законы сохранения относятся к так называемым изолированным системам. Будем в дальнейшем называть систему изолированной или замкнутой в том случае, если через контрольную поверхность - окружающую систему - нет переноса массы, количества движения и энергии. На изолированную систему не действуют внешние силы.

Закон сохранения массы для изолированной системы выражается в том, что масса m такой системы остается постоянной во все время движения, т.е. количество вещества остается постоянным или

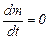. (3.24)

Общий закон сохранения массы применительно к сплошным средам получает свое выражение в уравнении неразрывности или сплошности движения. Для получения этого уравнения при отсутствии источников или стоков массы применим закон сохранения массы к некоторому элементарному объему , движущемуся вместе со средой, имеющей плотность 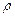. Так как

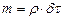(3.25)

то 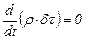, (3.26)

или 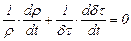. (3.27)

Относительное изменение объема в данной точке за единицу времени равно дивергенции вектора скорости в данной точке, т.е.

. (3.28)

Тогда уравнение неразрывности движения примет вид

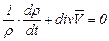. (3.29)

Если плотность зависит и от времени и от координат, т.е. 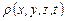, то

(3.30)

Подставив это выражение в (3.29), получим другой вид уравнения неразрывности (в проекциях на прямоугольные оси)

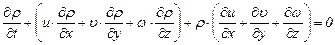(3.31)

или

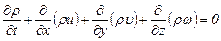. (3.32)

Последние слагаемые составляют дивергенцию 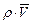, поэтому уравнение (3.29) в дифференциальной форме имеет вид

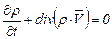. (3.33)

Для стационарного движения, при котором 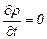, уравнение неразрывности примет вид

. (3.34)

При наиболее простом случае движения, когда плотность жидкости постоянна и не зависит от координат и времени, т.е. 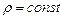, уравнение неразрывности будет иметь вид

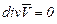. (3.35)

Уравнение неразрывности (сплошности) также может быть представлено в интегральной форме в виде

, (3.36)

где S - поверхность, ограничивающая объем .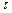

При установившемся движении для элементарной струйки идеальной жидкости уравнение неразрывности может быть представлено также в гидравлической форме в соответствии с выражением (3.15), а для полного живого сечения трубки тока конечных размеров при равномерном распределении параметров среды по сечению - выражением (3.21).

3.5. Вихревое и безвихревое (потенциальное) движения

Напомним некоторые дифференциальные операции с векторами, известные из векторного анализа. Для этого воспользуемся векторным оператором Гамильтона

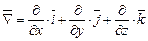(3.37)

и проделаем некоторые формальные операции.

Из векторной алгебры известно, что скалярное произведение орт будет

;

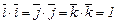, (3.38)

а их векторное произведение равно

;

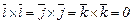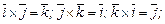
, (3.39)

поэтому получим следующие операции с оператором .

1. Действие оператора на скалярную функцию , равное

, (3.40)

называется градиентом скалярной фукнции. 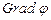есть вектор, который обладает, как будет показано далее, некоторыми особенностями, и называется он потенциальным вектором.

2. Скалярное произведение оператора на вектор

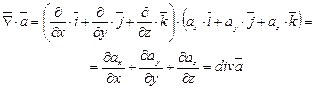(3.41)

есть величина скалярная и называется дивергенцией или расходимостью вектора.

3. Векторное произведение оператора на вектор

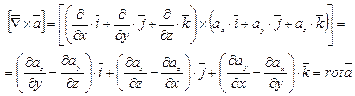(3.42)

есть величина векторная и называется она вихрем или ротором вектора.

Заметим, что скалярное произведение оператора на

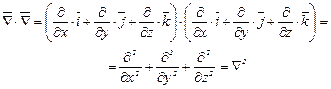(3.43)

есть оператор Лапласса. Применяя этот оператор к скалярной функции , получим

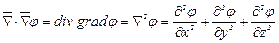. (3.44)

Пользуясь оператором Гамильтона, легко получить следующие дифференциальные операции второго порядка:

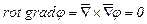; (3.45)

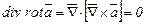. (3.46)

Очевидно, что первое выражение обращается в нуль потому, что векторное произведение параллельных векторов (и 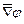) равно нулю, а второе - обращается в нуль потому, что здесь имеет место скалярное произведение взаимно перпендикулярных векторов: и .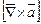

Применим указанные операции в механике сплошных сред. Для определения физического смысла величины вектора рассмотрим поле любой скалярной величины, встречающееся в механике (температура, плотность, давление и пр.). В скалярном поле характерными линиями, определяющими поле, являются линии равных значений рассматриваемой величины. Для температуры это изотермы, для давлений - изобары, для проекций скоростей - изотахи и т.д. В качестве примера на рис. 3.5 приведены изотахи для расходных составляющих скоростей в выходном сечении патрубка турбины.

Рис. 3.5. Изотахи в выходном сечении патрубка турбины

В непрерывном поле скалярной величины через любую точку пространства можно провести линию постоянного значения. При этом в каждой точке скалярного поля значение производной от рассматриваемой величины будет зависеть от выбора направления. По направлениям касательных к линиям постоянного значения производные равны нулю, а по нормали к этой линии производная будет иметь наибольшее значение. Градиент скалярной функции есть вектор, направленный по нормали к линии постоянного значения скалярной функции в сторону увеличения этой функции и равный по величине производной от функции по направлению указанной нормали.

Таким образом, видно, что градиенты скалярного поля составляют векторное поле.

Рассмотрим физический смысл вихря вектора скорости. Из ранее приведенного определения следует, что

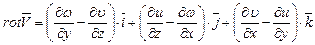. (3.47)

Напомним уже известное понятие вращения твердого тела. Пусть некоторое тело вращается с угловой скоростью вокруг оси z. Тогда из рис. 3.6 видно, что величина скорости точки тела М будет равна 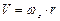, а ее проекции на оси х и у соответственно 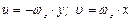и .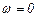

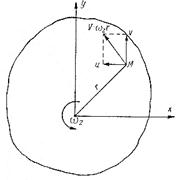
Рис. 3.6. Схема скоростей вращающегося тела

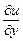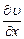Определив значения и , получим, что

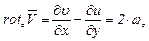, (3.48)

т.е. . (3.49)

Если аналогичным образом рассмотреть вращение твердого тела вокруг осей х и у, то соответственно найдем

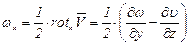; (3.50)

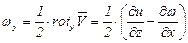. (3.51)

Следовательно, вихрь вектора скорости жидкой частицы может быть определен вектором угловой скорости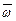

. (3.52)

а модуль этого вектора равен

. (3.53)

Дата добавления: 2014-01-06