Гидравлика 5 страница

Физически неравенство нулю значения в какой-либо точке потока означает, что в этой точке имеет место вращение элементарного объема. Никакого видимого вращения жидкости при этом в этой точке может и не быть. В качестве примера рассмотрим поток, в котором 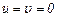, a 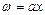. Очевидно, для такого потока 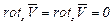, a . Следовательно, это поток вихревой, так как , хотя никакого видимого вращения потока нет. Таким образом, вихрь отражает наличие вращательного движения только для элементарного объема.

Например, наблюдая за движением лодки в воде, легко видеть вихри, образующиеся за кормой лодки. Но, согласно введенному определению вихря, вихревое движение жидкости будет иметь место не только за кормой лодки, но и в непосредственной близости к корпусу лодки, где скорость изменяется довольно сильно и .

Иногда вихревое движение отождествляют с турбулентным. Это совершенно разные понятия. Вихревое движение может быть и ламинарным и турбулентным, а, в свою очередь, ламинарное и турбулентное (осредненное) движения могут быть как вихревыми, так и безвихревыми.

Если вектор скорости есть потенциальный вектор, то, его можно представить в виде

. (3.54)

Следовательно, проекции скорости и будут равны

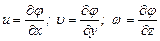. (3.55)

Последнее условие означает, что величина есть потенциал скорости .

Очевидно, что если вектор скорости имеет потенциал, то в соответствии с формулами (3.54) и (3.45) будем иметь

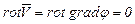. (3.56)

Такое движение, при котором , называется безвихревым или потенциальным движением жидкисти.

В гидродинамике широко применяется понятие циркуляции скорости. Если и векторном поле скоростей проведем отрезок кривой АВ (рис. 3.7), то криволинейный интеграл

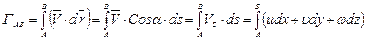(3.57)

определяет величину циркуляции вектора скорости по контуру s на участке АВ.

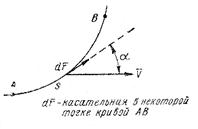
Рис. 3.7. Схема циркуляции скорости

Если кривая, по которой определяется циркуляция, замкнутая, то величина циркуляции определяется интегралом по замкнутому контуру

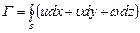. (3.58)

Легко видеть, что при наличии потенциала скоростей в векторном поле циркуляция скорости на участке АВ определяется разностью значений потенциала скоростей в точках А и В. Действительно, учитывая выражения (3.55), получим

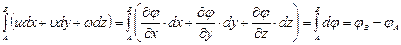.(3.59)

Когда контур АВ замкнутый и внутри не содержится никаких особенностей, то циркуляция по этому контуру будет равна нулю, так как .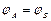

Вихри скоростей образуют векторное поле, поэтому в нем можно получить векторные линии и векторные трубки.

Линия, в каждой точке которой вихри вектора скорости или вектора угловых скоростей вращения частиц касательны к ней, называется вихревой линией.

Уравнение вихревых линий, как следует из выражения (3.12), будет

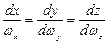. (3.60)

Если в пространстве, заполненном вихрями, взять некоторый замкнутый контур (не являющийся вихревой линией) и через каждую точку этого контура провести вихревые линии, то образуется вихревая поверхность. Часть жидкости, ограниченная этой поверхностью, называется вихревой трубкой. Когда замкнутый контур бесконечно мал, то вихревая трубка называется элементарной.

Из определения вихревой липни и вихревой поверхности следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю.

Следовательно, если ввести понятие о потоке вектора вихря скорости, равном в соответствии с формулой (3.16)

,

то поток вектора вихря скорости через вихревую поверхность равен нулю.

Из векторного анализа известно, что поток любого вектора через любую замкнутую поверхность, внутри которой нет особенностей, равен нулю. Из этой теоремы векторного анализа вытекает, что и поток вихря сквозь любую замкнутую поверхность тоже равен нулю

. (3.61)

Выделим в вихревой трубке (рис. 3.8) некоторую замкнутую поверхность, образованную двумя любыми поперечными сечениям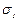и и и боковой поверхностью .

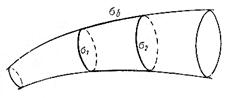
Рис. 3.8. Схема вихревой трубки

Так как поток вихря по боковой поверхности равен нулю, то, согласно формуле (3.61), следует

. (3.62)

Из полученного равенства вытекает следующее свойство вихревых трубок, известное в кинематике, как вторая теорема Гельмгольца: поток вектора вихря скорости сквозь произвольно проведенное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки.

Из этой теоремы следует, что поток вихря есть величина, характерная для всей вихревой трубки. Поэтому поток вихря принимают за характеристику вихревой трубки и называют интенсивностью вихревой трубки

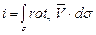. (3.63)

Иногда интенсивность вихревой трубки выражают через угловую скорость следующим образом:

. (3.64)

Если величина вихря постоянна по поперечному сечению вихревой трубки, то вторую теорему Гельмгольца можно записать в виде

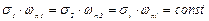. (3.65)

Из этой теоремы вытекают очень важные следствия:

1) сечение вихревой трубки нигде не может стать равным нулю, так как в этом сечении скорость вращения частиц должна стать бесконечной, что физически невозможно;

2) вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца (рис. 3.9), либо «опираются» на стенку или на свободную поверхность.

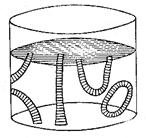
Рис. 3.9. Схемы вихревых колец

К последнему типу вихрей принадлежат наблюдаемые в природе водяные и воздушные смерчи. Прибор, иллюстрирующий образование вихря, показан на рис. 3.10.

Рис. 3.10. Прибор для образования вихря

Вращение шкива, имеющего несколько радиальных перегородок, закручивает воздух. В области разрежения, создаваемого воздушным вихрем, вода поднимается и образует искусственный смерч.

В идеальной жидкости при наличии массовых сил, обладающих однозначным потенциалом, интенсивность вихря не меняется со временем. Таким образом, вихри идеальной жидкости не могут менять в пространстве и во времени своей интенсивности. Они должны существовать вечно, они не могут возникать и вырождаться. В действительности, в реальной жидкости из-за наличия вязкости вихри зарождаются и затем диффундируют, т.е. вырождаются.

Из теоретической механики известно, что скорость любой точки М твердого тела определяется геометрической суммой скорости поступательного движения вместе с некоторым полюсом О и скорости вращения вокруг мгновенной оси, проходящей через полюс О, т.е.

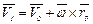, (3.66)

где 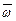- угловая скорость вращения;

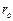- радиус-вектор точки М.

Аналогичная теорема, являясь основной теоремой кинематики, имеет место и для скоростей движения элементарных жидких объемов. Эта теорема гласит: скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и скорости деформации , т. е.

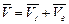. (3.67)

Скорость квазитвердого движения, как следует из формулы (3.66), в свою очередь складывается из поступательной скорости и скорости вращения.

Для доказательства этой теоремы определим в данный момент времени поле скоростей в окрестности точки (рис. 3.11).

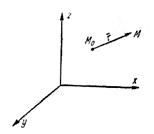
Рис. 3.11. Поле скоростей в окрестностях точки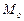

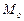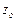Пусть в точке с координатами и скорости будут иметь значения 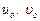и .

В соответствии с рядом Тейлора можно найти значение скоростей и в точке , расположенной в окрестности точки 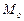. С точностью до малых первого порядка они будут равны

;

; (3.68)

,

где .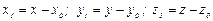

Прибавив и вычтя в первом уравнении (3.68) величину

, (3.69)

получим

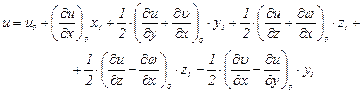(3.70)

Для дальнейших преобразований введем следующие обозначения:

;

;

;

;

;

;

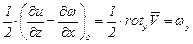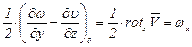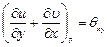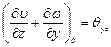. (3.71)

Тогда уравнение (3.70) будет

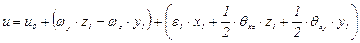, (3.72)

а остальные два уравнения (3.68) после аналогичных преобразований примут вид

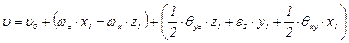; (3.73)

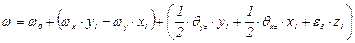. (3.74)

Первые два слагаемых правой части полученных уравнений можно рассматривать как скорости квазитвердого движения, третьи слагаемые являются скоростями деформации элементарного объема.

Так как, согласно рис 3.11,

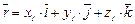, (3.75)

то

;

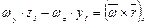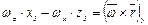; (3.76)

.

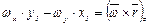Для характеристики скорости деформации введем функцию F, равную

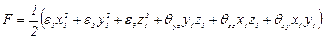, (3.77)

Тогда

;

; (3.78)

.

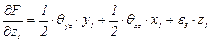Используя выражения (3.76) и (3.78), окончательно получим

;

; (3.79)

,

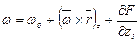или в векторном виде

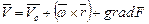, (3.80)

где - скорость поступательного движения;

- скорость вращательного движения вокруг мгновенной оси с угловой скоростью ;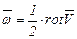

grad F - скорость чистой деформации.

Скорость деформации жидкой частицы в точке М определяется следующей таблицей:

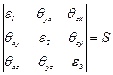. (3.81)

Таблица S называется тензором скоростей деформации, a - компонентами или составляющими тензора скоростей деформации.

При этом 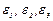, расположенные на диагонали таблицы, характеризуют скорости относительного удлинения (сжатия) жидких отрезков, a - скорости перекосов элементарного объема. Рассмотрим детально отдельные составляющие тензора скоростей деформаций.

Возьмем сферическую частицу движущейся жидкости (рис. 3.12) и посмотрим, что с ней произойдет через время dt.

Рис. 3.12. Схема деформации сферической частицы

жидкости

Сферическая частица в момент времени t имела объем 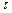, через время dt эта частица может остаться сферической или измениться, но измениться незначительно, ибо время dt очень мало. Пусть - объем эллипсоида с полуосями и с, образовавшегося из сферы за время dt. Найдем изменение объема. Обычно берут относительное изменение объема в единицу времени, т.е. .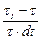

Объем шара равен

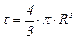, (3.82)

объем эллипсоида запишется

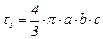, (3.83)

причем его полуоси будут

;

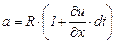; (3.84)

,

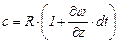где - изменение скорости по осям координат.

Тогда

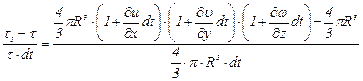. (3.85)

После раскрытия скобок и пренебрежения величинами второго и третьего порядка малости будем иметь

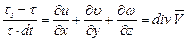. (3.86)

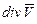характеризует собой расходимость вектора скорости. Используя старые обозначения

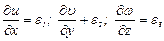. (3.87)

получим

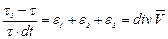. (3.88)

Отсюда видно, что совокупность диагональных составляющих тензора скоростей деформации (3.81) выражает расходимость вектора скорости, характеризующего собой скорость (быстроту) относительного изменения объема жидкой частицы.

Для характеристики компонентов тензора скоростей деформации рассмотрим детально один из них, например . Эта величина характеризует скорость деформации сдвига жидкой частицы в плоскости ху.

Пусть в некоторый момент времени жидкая частица будет иметь в плоскости ху форму квадрата со сторонами dx и dy (рис. 3.13).

Рис. 3.13. Схема деформации жидкой частицы

Так как скорости в вершинах квадрата будут неодинаковы (рис. 3.13, а), то через единицу времени рассматриваемый квадрат примет форму параллелограмма (рис. 3.13, б). При этом угол сдвига 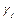между осью игреков и стороной О'С' будет равен

, (3.89)

а угол между осью иксов и стороной О'А' соответственно

. (3.90)

Так как мы рассмотрели изменение прямого угла СОА за единицу времени, то величина

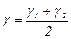(3.91)

будет характеризовать скорость изменения первоначального угла АОС. Следовательно,

, (3.92)

т.е. характеризует скорость деформации скашивания угла или сдвига в плоскости ху.

Аналогичным образом можно показать, что и характеризуют скорости деформации сдвига в плоскостях уz и хz.

Таким образом, скорость деформации элементарной жидкой частицы полностью определяется тензором (3.81).

Второй важной кинематической теоремой о вихрях является теорема Стокса: интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру, один раз опоясывающему вихревую трубку. Докажем эту теорему для более общего случая с такой формулировкой: поток вектора вихря скорости через любую поверхность, опирающуюся на некоторый замкнутый контур, равен циркуляции скорости по этому контуру.

Вначале определим величину циркуляции скорости по некоторому бесконечно малому контуру, который находится в движущейся жидкости, имеющей непрерывно распределенные вихри. Пусть контур ОСВАО (рис. 3.13, а) лежит в плоскости ху и имеет стороны dx и dy. Если в точке О проекции скоростей будут 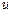и 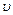, то в точках С и А величины скоростей, совпадающих по направлению со сторонами СВ и АВ, равны соответственно

; (3.93)

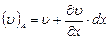. (3.94)

Тогда циркуляция по контуру ОСВАО будет равна

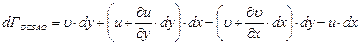(3.95)

или, раскрывая скобки и производя сокращение, получим

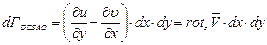. (3.96)

Так как является проекцией вихря на ось z, нормальную к площадке dxdy, то правая часть последнего равенства является потоком вектора вихря скорости через площадку dxdy. Проделав аналогичные вычисления для площадок dxdz и dydz и распространив эти результаты на элементарную площадку 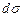, произвольно расположенную в пространстве, получим

. (3.97)

Последнее соотношение означает, что циркуляция по бесконечно малому прямоугольному контуру равна потоку вихря через площадку, ограниченную этим контуром, или интенсивности элементарной вихревой трубки.

Если теперь возьмем произвольный плоский контур с любой конечной площадью, то, разбив, как это показано на рис. 3.14, всю площадь на элементарные прямоугольники и вычислив циркуляцию по контурам этих прямоугольников, в результате суммирования по всей площади получим циркуляцию вдоль всего контура, равную

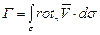. (3.98)

Рис. 3.14. Циркуляция скорости через плоский контур

и произвольную поверхность

Полученную формулу можно применить не только для плоской площадки, а и для некоторой произвольной поверхности (рис. 3.14). Разбив эту поверхность на бесконечно большое количество бесконечно малых площадок 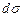, получим величину циркуляции для каждой площадки (считая ее плоской), равную

. (3.99)

Суммируя циркуляции по элементарным площадкам, получим циркуляцию по поверхности

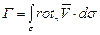. (3.100)

Таким образом, теорему Стокса можно считать доказанной для произвольного контура, а следовательно, и для контура, опоясывающего вихревую трубку.

Формула (3.100) после подстановки выражения для циркуляции (3.57) будет иметь вид

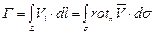. (3.101)

Заменив вектор скорости на некоторый вектор а, получим известную из векторного анализа формулу Стокса, связывающую интеграл по контуру с интегралом по поверхности, опирающейся на этот контур

, (3.102)

где .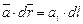

4. СИЛЫ, ДЕЙСТВУЮЩИЕ В ЖИДКОСТЯХ

4.1. Массовые и поверхностные силы

Вследствие текучести (подвижности частиц) в жидкости действуют силы не сосредоточенные, а непрерывно распределенные по ее объему (массе) или поверхности. Существует много различных принципов классификации сил, приложенных к частицам сплошных сред. В зависимости от области приложения силы делятся на внутренние и внешние. По своей природе или по характеру действия силы делятся на массовые (или объемные) и поверхностные.

Массовые, или объемные, силы пропорциональны массе выделенного объема или при постоянной плотности среды пропорциональны объему; они действуют на все частицы среды этого объема. Массовыми, или объемными, силами являются: силы веса, все электромагнитные, электрические объемные силы, в том числе силы Лоренца и силы электростатического притяжения, и различные силы инерции (Кориолисова сила, центробежная сила и др.).

Поверхностные силы действуют лишь на поверхность выделенного объема. Обычно поверхностные силы делятся на две категории: а) поверхностные силы, направленные по нормали к выделенной площадке; б) поверхностные силы, направленные по касательной к этой площадке.

В покоящейся жидкости поверхностные силы направлены по нормали к элементу поверхности выделенного объема. В движущейся вязкой жидкости имеют место и нормальные, и касательные составляющие поверхностных сил. Последние из них определяют силы трения.

Распределение массовых сил в некотором объеме 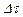задается вектором плотности массовой силы, равным пределу отношения главного вектора массовых сил 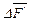, приложенных к частицам некоторого объема с массой , к этой массе при стремлении последней к нулю, т.е.

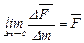. (4.1)

Для характеристики распределения массовых сил обычно пользуются осредненным значением вектора плотности массовых сил, равным отношению главного вектора массовых сил к величине массы, т.е.

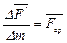. (4.2)

Очевидно, размерность плотности массовой силы будет размерностью ускорения. Действительно

.

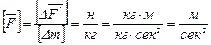4.2. Напряжения поверхностных сил

В отличие от объемных сил, вектор которых для частицы среды определяется однозначно, величина поверхностной силы в точке, в общем случае, зависит от выбора направления элементарной площадки.

Обычно рассматриваются не сами поверхностные силы, а их напряжения, т.е.

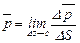, (4.3)

где 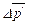- главный вектор поверхностных сил, приложенных к некоторой площадке .

Размерность напряжений будет

.

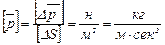В практике часто пользуются единицей измерения давления, называемой технической атмосферой, которая по величине равна

1 am = 736 мм pт. cm = 10 м вод. cm = 10 000 мм вод. cm.

В технике пользовались размерностью кгс/м² (кгс - килограммсила в старой системе единиц). Очевидно, что

,

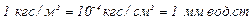поэтому величину давления часто выражают в миллиметрах водяного столба.

В международной системе единиц СИ за единицу давления принимается давление силы в 1 ньютон на 1 кв. метр. Эта единица равна

.

В виду того, что эта единица очень мала, можно применять укрупненные единицы давления: 1 килоньютон на 1 кв. метр (кн/м²), 1 меганьютон на 1 кв. метр (мн/м²) и внесистемную единицу давления бар (бар), равный 10⁵ н/м², а также дольные единицы бара -миллибар (мбар) и микробар (мкбар). Очевидно, что

.

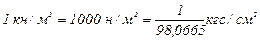Рассмотрим условие равновесия элементарного жидкого объема, находящегося под действием поверхностных и массовых сил. Для этого в покоящейся жидкости выделим некоторый элементарный тетраэдр с длиной ребер dx, dy, dz (рис. 4.1).

Очевидно, три грани тетраэдра лежат в координатных плоскостях, а четвертая, наклонная грань, является как бы замыкающей. Пусть площади соответствующих граней будут 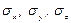и .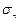

Дата добавления: 2014-01-06