Гидравлика 6 страница

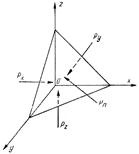
Рис. 4.1. Схема элементарного тетраэдра

По ранее введенному определению поверхностные силы элементарного тетраэдра пропорциональны произведению двух длин сторон тетраэдра, а массовые силы пропорциональны объему. Следовательно, массовыми силами как величинами третьего порядка малости можно пренебречь по сравнению с поверхностными силами - величинами второго порядка малости.

Согласно основному свойству жидкостей, находящихся в равновесии, поверхностные силы, заменяющие действие отброшенной части жидкости при выделении тетраэдра, будут направлены по нормали к граням тетраэдра. Таким образом, эти силы являются силами давления. Если обозначить величины сил давления, приложенных к граням, 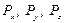и (рис. 4.1), то для сохранения условий равновесия, известных из статики твердого тела, необходимо, чтобы сумма всех внешних сил или сумма проекций всех внешних сил на координатные оси была равна нулю. Для рассматриваемого тетраэдра это условие можно записать в виде

;

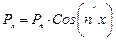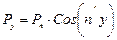; (4.4)

,

где n - орт нормали к наклонной грани.

Если первое уравнение системы разделим на величину площадки 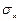, а второе и третье соответственно на 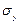и 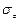, то получим условие равновесия в величинах напряжений сил давления

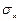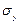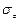Но из рис. 4.1 видно, что , и - проекции наклонной грани на плоскости yОz, xОz и хОy, т.е.

;

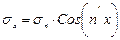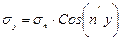; (4.5)

.

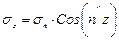Подставив эти величины в правые части предшествующих уравнений, окончательно получим

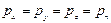. (4.6)

Так как при выделении элементарного тетраэдра никаких ограничений относительно его положения в неподвижной жидкости не накладывалось, то из последнего уравнения следует, что в покоящейся жидкости величина напряжения силы давления, называемая гидростатическим давлением в точке, не зависит от ориентации площадки, к которой приложено давление. Приведенные выводы выражают собой известный закон Паскаля, гласящий, что «...давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях». Очевидно, что если давление не зависит от ориентации площадки, проходящей через данную точку, и определяется только положением точки в жидкости, то, следовательно, давление р есть функция только координат: р = f (х, у, z).

Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает.

4.3. Напряженное состояние

Поверхностные силы, действующие в движущихся сплошных средах, существенно отличаются от поверхностных сил, действующих в покоящейся среде. Это отличие заключается не только в появлении касательных составляющих, которые в покоящейся жидкости отсутствуют, а также и в том, что нормальные составляющие сил изменяют свою величину. Найдем величины, определяющие поверхностные напряжения в некоторой точке сплошной среды. Для этого рассмотрим в движущейся жидкости элементарный тетраэдр с вершиной в точке О (рис. 4.2).

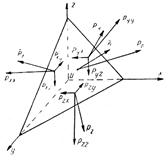
Рис. 4.2. Расчетная схема элементарного тетраэдра

Площади боковых граней тетраэдра равны , причем индексы означают ось, перпендикулярно которой расположена грань. Наклонная грань имеет площадь, равную 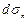; n - нормаль к этой грани. К каждой из рассматриваемых граней будут приложены поверхностные силы, в общем случае направленные под некоторым углом к грани. Обозначим вектор напряжения поверхностных сил, приложенных к грани, перпендикулярной оси х, через 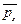соответственно к граням, нормальным к осям у и z, через 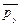и . 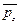К наклонной грани приложено напряжение 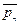. Как видно из рис. 4.2,

;

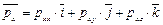; (4.7)

.

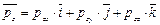Второй индекс у проекций напряжений означает ось, на которую проектируются векторы напряжени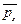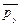й , и .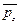

Зная 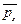, 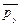и 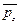в соответствии с выражениями (4.7), можно определить вектор поверхностных сил 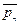, приложенный к площадке с любым заданным направлением орта нормали n.

Действительно, написав уравнение движения центра инерции тетраэдра с массой dm, получим

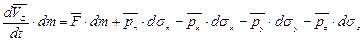, (4.8)

где 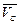- скорость центра инерции тетраэдра;

F - плотность массовых сил.

Члены в уравнении, содержащие элементарную массу, являются величинами третьего порядка малости, в то время как остальные - второго порядка малости. Поэтому величинами, содержащими dm, пренебрегаем. Получим

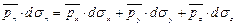. (4.9)

Из рис. 4.2 видно, что

;

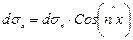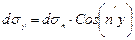; (4.10)

,

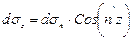поэтому

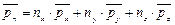, (4.11)

где ;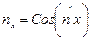

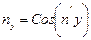; (4.12)

.

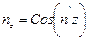Используя формулу (4.11), можно получить проекции вектора напряжений поверхностных сил, приложенных к площадке с любым заданным направлением n, на координатные оси х, у и z:

;

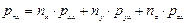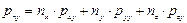; (4.13)

;

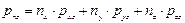Из выражений (4.7) и (4.11) видно, что напряжение в точке определяется совокупностью величин

. (4.14)

Таблица величин, определяющих напряженное состояние в точке, называется тензором напряжений. Составляющие 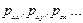будем называть компонентами тензора напряжений или просто компонентами напряжений.

Из рис. 4.2 видно, что диагональные составляющие тензора 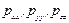есть нормальные составляющие напряжений поверхностных сил, а 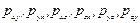- касательные составляющие напряжений.

Докажем, что компоненты касательных напряжений, симметричные относительно главной диагонали таблицы (4.14), попарно равны

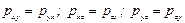. (4.15)

Рассмотрим элементарный жидкий параллелепипед со сторонами dx, dy, dz (рис. 4.3), находящийся в равновесии.

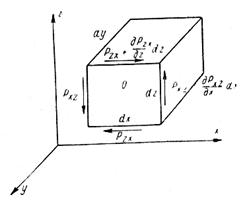
Рис. 4.3. Расчетная схема элементарного параллелепипеда

Составим уравнение моментов сил, действующих на грани параллелепипеда, относительно оси, перпендикулярной грани dx, dz и проходящей через центр тяжести этой грани О,

(4.16)

Если пренебречь величинами четвертого порядка малости, то последнее уравнение примет вид

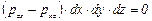. (4.17)

Следовательно,

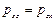. (4.18)

Аналогично доказывается равенство других касательных напряжений

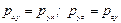. (4.19)

5. ОБЩИЕ ЗАКОНЫ И УРАВНЕНИЯ СТАТИКИ

И ДИНАМИКИ ЖИДКОСТЕЙ И ГАЗОВ

5.1. Уравнения движения в напряжениях

Это уравнение можно получить путем применения теоремы об изменении количеств движения к некоторому элементарному объему 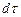сплошной среды. В соответствии с ранее сказанным все внешние силы складываются из массовых и поверхностных. Следовательно, главный вектор внешних сил можно представить как сумму двух указанных главных векторов сил: объемных 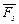и поверхностных 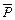. Тогда в соответствии с теоремой об изменении количеств движения получим

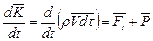. (5.1)

Но 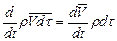, (5.2)

так как есть масса жидкости в объеме 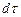, которая остается постоянной во все время движения.

Используя последнее соотношение, получим выражение известного в механике принципа Даламбера

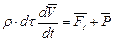, (5.3)

согласно которому уравнение динамики можно свести к уравнению статики, если к внешним силам присоединить силы инерции.

Применим теорему об изменении количеств движения к массе, заключенной в объеме элементарного параллелепипеда со сторонами dx, dy и dz. Тогда вектор массовых сил можно представить в виде

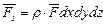, (5.4)

где - вектор массовых сил, отнесенный к единице массы.

Найдем теперь главный вектор поверхностных сил. На рис. 5.1 показаны напряжения поверхностных сил, приложенных к граням, нормальным к оси х. Легко показать аналогичную схему напряжений, приложенных к граням, нормальным к осям у и z.

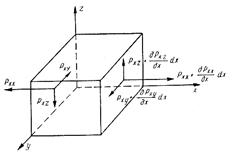
Рис. 5.1. Схема напряжений поверхностных сил

Спроектируем составляющие поверхностных сил на ось х. Рассмотрение сил, приложенных к граням, нормальным к оси х приводит к выражению

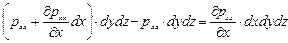, (5.5)

к граням, нормальным к оси у, -

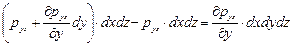, (5.6)

к граням, нормальным к оси z -

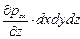. (5.7)

Таким образом, проекция главного вектора поверхностных сил на ось х будет

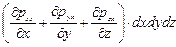. (5.8)

Соответственно проектирование на оси у и z дает

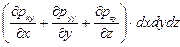; (5.9)

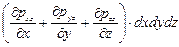. (5.10)

Тогда в соответствии с формулой (5.3) получим уравнения, отнесенные к единице объема, в проекциях на прямоугольную систему координат

;

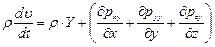; (5.11)

.

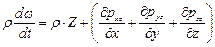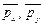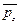Так как вектора напряжений поверхностных сил и , приложенных к площадкам, нормальным осям х, у и z, по формулам (4.7) равны

;

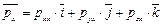; (5.12)

,

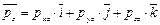то уравнение в векторном виде, соответствующее уравнениям в проекциях (5.11), будет

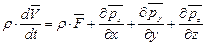. (5.13)

Уравнения (5.11) и (5.13) являются уравнениями движения сплошных сред в напряжениях; в дальнейшем их будем называть уравнениями в напряжениях.

5.2. Уравнения гидростатики в форме Эйлера и их интегралы

Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы, например, силы инерции переносного движения и т.п. Если сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия, которое называют относительным покоем.

В неподвижной жидкости возьмем произвольную точку М с координатами x, у и z и давлением р (рис. 5.2). Систему координат будем считать жестко связанной с сосудом, содержащим жидкость.

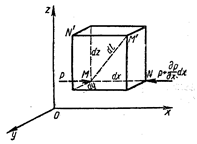
Рис. 5.2. Схема для вывода дифференциальных уравнений

равновесия жидкости

Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz. Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила , составляющие которой, отнесенные к единице массы, равны X, Y и Z. Тогда массовые силы, действующие на выделенный объем в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объема.

Давление р есть функция координат x, y и z, но вблизи точки М по всем трем граням параллелепипеда оно одинаково, что вытекает из доказанного выше свойства гидростатического давления. При переходе от точки М, например, к точке N изменяется лишь координата x на бесконечно малую величину dx, в связи с чем функция р получает приращение, равное частному дифференциалу (др /дх) dx, поэтому давление в точке N равно
р + (др /дх) dx, где др /дх - градиент давления вблизи точки М в направлении оси x. Рассматривая давления в других соответствующих точках граней, нормальных к оси х, например в точках N' и М', видим, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину

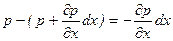. (5.14)

Ввиду этого разность сил давления, действующих на параллелепипед в направлении оси х, равна указанной величине, умноженной на площадь грани: .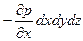

Аналогичным образом, но через градиенты давления др/ду и др/дz выразим разности сил давления, действующие на параллелепипед в направлении двух других осей.

На выделенный параллелепипед действуют лишь указанные массовые силы и силы давления, поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей запишем в следующем виде:

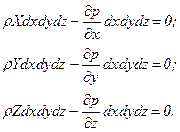(5.15)

Разделим эти уравнения на массу rdxdydz параллелепипеда и перейдем к пределу, устремляя dx, dy и dz к нулю, т.е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке М:

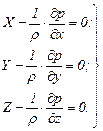(5.16)

Уравнения (5.16) являются основными уравнениями гидростатики и часто называются уравнениями равновесия Эйлера для жидкости и газа.

Так как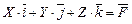

и ,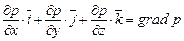

то система уравнений (5.16) может быть представлена в векторном виде

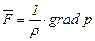. (5.17)

При относительном покое вектор плотности массовых сил включает силы инерции.

Поскольку массовые силы в большинстве случаев обладают потенциалом, то

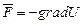, (5.18)

где U - потенциал массовых сил или силовая функция.

Тогда уравнению (5.17) можно придать вид

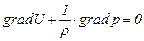. (5.19)

Общим интегралом этого уравнения в случаях, когда , является соотношение

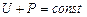, (5.20)

где 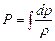- функция давления (для несжимаемой жидкости (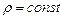) ; для сжимаемой - вид функции P зависит от связи между р и ).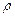

Если из числа массовых сил на жидкость действует только гравитационная (тяжелая жидкость), то

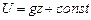, (5.21)

где z - координата, отсчитываемая вертикально вверх.

Для тяжелой несжимаемой жидкости интеграл (5.20) принимает вид

. (5.22)

Эта формула выражает гидростатический закон распределения давлений.

Для практического пользования удобнее вместо приведенной системы уравнений (5.16) иметь одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений на dx, второе - на dy, третье - на dz и, сложив все три уравнения, получим:

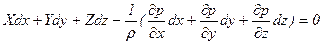. (5.23)

Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т.е. функции р(х, у, z), поэтому предыдущее уравнение можно переписать в виде:

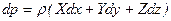. (5.24)

Следовательно, при наличии равновесия полным дифференциалом должна быть и правая часть уравнения (5.24). В частности, при постоянной плотности (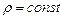) получим

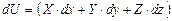. (5.25)

Из последнего условия видно, что массовые силы имеют потенциал U и проекции массовых сил можно выразить через потенциал в виде

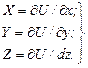(5.26)

Тогда уравнение (5.24) запишется в виде

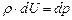. (5.27)

Следовательно, жидкость может находиться в равновесии только в том случае, если массовые силы, действующие в ней, имеют потенциал, т.е. проекции массовых сил удовлетворяют условию (5.26).

Поверхность, в каждой точке которой давление постоянно, называют поверхностью уровня. Если в уравнении (5.24) положить , то уравнение поверхности уровня будет

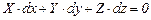, (5.28)

или 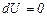. (5.29)

5.3. Напряжения сил вязкости, обобщенная гипотеза Ньютона

Рассмотрим механику переноса количества движения, вследствие которого возникают поверхностные силы трения в движущихся жидкостях и газах. В отличие от идеальных жидкостей, в которых имеют место только нормальные составляющие поверхностных сил, в реальных жидкостях наличие вязкости вызывает появление касательных составляющих и изменяет величину нормальных составляющих.

В покоящейся жидкости, а также в жидкости, совершающей поступательное движение или вращающейся как одно целое, наличие вязкости не вызывает касательных сил, а нормальные составляющие могут определяться так же, как и для идеальной жидкости.

Вязкость вызывает появление внутреннего трения только в том случае, когда происходит движение частиц жидкости относительно друг друга. Если вспомнить, что по первой теореме Гельмгольца скорость частицы складывается из поступательной, вращательной и деформационной составляющих, то, следовательно, внутреннее трение в жидкости может возникать только при наличии деформации жидкого объема. Тогда естественно, что компоненты напряжения поверхностных сил должны зависеть от составляющих скоростей деформации.

Еще Ньютон показал, что в случае движения реальной жидкости параллельно некоторой плоскости касательное напряжение между двумя слоями, отнесенное к единице длины, будет пропорционально производной от скорости по нормали к направлению движения

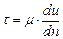. (5.30)

Если задать прямолинейное движение в плоскости ху параллельно оси x, то тогда величина 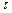будет являться компонентой напряжения 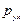и равна

, (5.31)

при направлении движения параллельно оси у получим

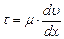. (5.32)

Следовательно, при произвольном движении в плоскости ху напряжение сил трения, равное одной из касательных компонент 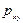, входящих в тензор напряжений, будет равно

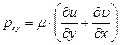. (5.33)

Соответственно для плоскостей xz и уz получим

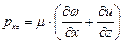; (5.34)

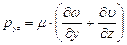. (5.35)

Соотношения (5.33) - (5.35) являются обобщением формулы Ньютона (5.30) и, таким образом, выражают обобщенный закон Ньютона для касательных напряжений.

Если касательные напряжения выражать через скорости скашивания углов, то обобщенный закон Ньютона будет гласить, что в общем случае касательные напряжения будут пропорциональны скорости скашивания углов. Коэффициенты пропорциональности 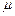во всех случаях являются коэффициентами вязкости. Обобщенный закон Ньютона и многочисленные последующие опыты позволяют сделать вывод о том, что при не очень больших градиентах скоростей компоненты тензора напряжений являются линейными функциями от составляющих тензора скоростей деформации. Так как в гидромеханике обычно рассматриваются изотропные жидкости, то можно считать, что коэффициенты этих функций не зависят от выбора системы координат.

Для нахождения нормальных составляющих напряжений необходимо, кроме обобщенного закона Ньютона о линейности связи напряжений и скоростей деформации, сделать еще допущение о том, что компоненты нормальных напряжений при отсутствии вязкости должны приводиться к нормальным напряжениям, не зависящим от выбора направления площадки. Обозначим эти не зависящие от направления площадки напряжения временно буквой А. Тогда компоненты нормальных напряжений

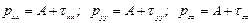. (5.36)

При этом 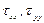и 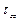отличны от нуля только в вязкой жидкости. Если линейную связь между величинами 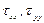,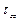и соответствующими компонентами тензора скоростей деформаций представить в виде

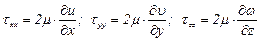, (5.37)

то выражения для 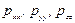запишутся

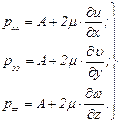(5.38)

Величина А, не зависящая от выбора направления площадки, т.е. одинаковая для всех нормальных компонент напряжения, может быть найдена из соотношений (5.38)

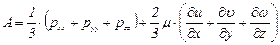. (5.39)

Если (как и в идеальной жидкости) принять для вязкой жидкости или газа допущение, что давление в точке есть взятое с обратным знаком среднее арифметическое трех нормальных напряжений, приложенных к взаимно перпендикулярным площадкам в этой точке, то

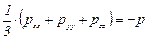, (5.40)

и величина А будет равна

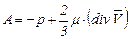. (5.41)

Подставив найденное значение для А в соотношения (5.38), окончательно получим выражение обобщенного закона Ньютона для нормальных составляющих напряжений

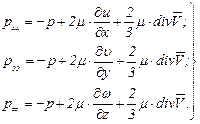(5.42)

Таким образом, соотношения (5.33) - (5.35) и (5.42) выражают обобщенный закон Ньютона для связи напряжений и скоростей деформаций.

Жидкости, у которых связи компонентов тензора напряжения и компонентов тензора скоростей деформации выражаются соотношениями (5.33) - (5.35) и (5.42), называются ньютоновскими или просто вязкими жидкостями. Опытом установлено, что эти соотношения сохраняются для всех газов и большинства реальных жидкостей, таких как вода, спирты, керосин, жидкие металлы, многие масла.

Дата добавления: 2014-01-06