Гидравлика 7 страница

5.4. Уравнение Навье-Стокса для вязкой жидкости

Рассмотрим изотермическое движение вязкой несжимаемой жидкости. В этом случае плотность и вязкость будут величинами постоянными.

Подставим выражения компонент напряжений в соответствии с формулами (5.33) - (5.35) и (5.42) в уравнения в напряжениях (5.11) и, учитывая, что для несжимаемой жидкости

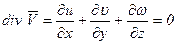, (5.43)

получим уравнение движения вязкой несжимаемой жидкости. Так, для проекции на ось х найдем

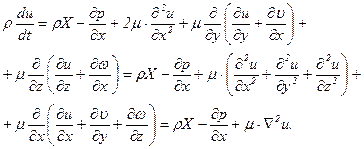(5.44)

Проделав аналогичные преобразования с двумя другими уравнениями (5.11), будем иметь систему уравнений

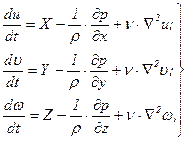(5.45)

где 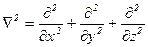- оператор Лапласа.

Уравнения (5.43) и (5.45) представляют собой замкнутую систему с четырьмя неизвестными 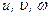и р. Величины 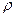и 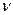, а также проекции массовых сил X, У и Z должны быть заданы.

Вспоминая выражение для ускорения (3.10), видим, что уравнения (5.45) представляют собой нелинейные дифференциальные уравнения в частных производных второго порядка. В векторной форме они имеют вид

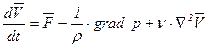, (5.46)

где 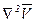- вектор с проекциями 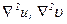и .

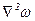Уравнения (5.45) впервые были получены в 1845 г. Сто-ксом и поэтому часто называются уравнениями Стокса.

Для решения системы (5.45) следует задать граничные условия. При наличии же локальных составляющих ускорения, т.е. в нестационарном потоке, необходимы и начальные условия.

Начальные условия ставятся так же, как и для идеальной жидкости, в виде распределения скоростей во всей рассматриваемой области в момент времени 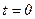, т.е. задается вид функций

.

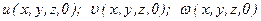Граничные условия как с математической, так и чисто физической стороны имеют весьма важное значение. Различие между движением идеальной и реальной жидкостями определяется не только различием самих уравнений, но и видом граничных условий. Обычно граничные условия задаются на поверхности обтекаемого тела и на бесконечности, в невозмущенной жидкости. На бесконечности, как правило, считают известными величины скорости и давления, а для внутренней задачи - расход жидкости.

Вид граничных условий на поверхности зависит от того, движется ли тело в потоке или тело неподвижно, а поток на него набегает. Рассмотрим отдельно значение нормальной и касательной составляющих скоростей на поверхности обтекаемого тела.

Граничные условия для нормальной составляющей определяются непроницаемостью твердой стенки. Так как через твердую стенку тела жидкость не перетекает, то эту стенку можно считать нулевой линией тока при движении как идеальной, так и реальной жидкостей. Отсутствие перетекания через линию или поверхность тока и есть граничное условие для нормальной составляющей скорости.

Граничное условие для касательной составляющей определяется из условий прилипания к стенке частиц жидкости или газа вследствие наличия вязкости, т.е. скорость жидкости на поверхности неподвижного обтекаемого тела должна равняться нулю, а для движущегося тела она должна быть равна скоростям соответствующих точек движущейся поверхности.

Для разреженных газов длина свободного пробега молекулы l не очень мала по сравнению с характерным размером b обтекаемого тела, т.е. 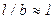, что наблюдается в некоторых вакуумных установках и в атмосфере на высоте 100 - 140 км. В этом случае, на поверхности тел происходит не полное прилипание, а течение со скольжением. Следовательно, граничные условия для касательной составляющей будут другие.

Часто тип граничных условий для любого уравнения в частных производных, называют именами известных ученых: Дирихле, Неймана или Робина. Условие Дирихле соответству ет случаю, когда на границе замкнутой области задано значение искомой функции, т.е. и = f. Если на границе замкнутой области задано значение не самой искомой функции, а лишь ее производной по нормали, т.е. ди1дп= f, то такое граничное условие называют условием Неймана. Смешанные граничные условия Дирихле и Неймана в виде ди / дп + ku = f, где k > 0, носят название граничного условия Робина.

5.5. Примеры аналитических решений уравнений Навье-

Стокса для ламинарного движения в цилиндрических трубах

В качестве первого примера интегрирования уравнения Стокса рассмотрим ламинарное стабилизованное движение несжимаемой жидкости в круглой цилиндрической трубе.

Под стабилизованным движением будем понимать такое стационарное движение, при котором скорость потока и профиль скоростей не зависят от продольной координаты. Следовательно, если направление движения совпадает с осью х, то проекции скоростей на оси у и z будут равны нулю, а проекция скорости на ось х будет зависеть только от у и z. Такое движение будет иметь место на плоской стенке или в цилиндрической трубе на значительном расстоянии от входа.

Если направление потока в трубе произвольного сечения совместить с осью х и считать, что для стабилизованного движения составляющие скоросте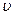й и 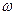отсутствуют, то в общем случае будем иметь

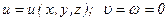и .

И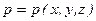спользуя уравнение неразрывности движения, получим, что ди / дх = 0 и, следовательно, скорость в трубе не зависит от координаты х. Последнее является условием для стабилизованного движения.

Уравнение Стокса после подстановки значени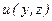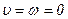й , и 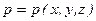и пренебрежения массовыми силами будет иметь вид

;

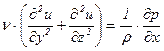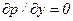и .

И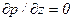з последних уравнений следует: 1) величина давления не зависит от поперечных координат у и z и есть функция только координаты х, т.е., в частности, в круглой трубе давление меняется только вдоль оси, а следовательно, постоянно в каждом сечении и не зависит от радиуса; 2) так как левая часть первого уравнения зависит только от у и z, а правая часть не зависит ни от у, ни от z, то, следовательно, и правая и левая части этого уравнения должны быть равны одной и той же постоянной величине, т.е.

dp / dx = const. (5.47)

Таким образом, уравнение Стокса для стабилизованного движения жидкости в цилиндрической трубе произвольного сечения или в более общем случае для прямолинейно параллельного стабилизованного движения вдоль оси х будет иметь вид

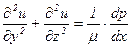. (5.48)

Если прямоугольную систему координат заменить на цилиндрическую, в которо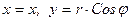й и 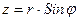, то уравнение (5.48) в цилиндрической системе координат будет

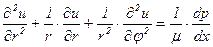. (5.49)

Вид решения уравнений (5.48) или (5.49) определяется граничными условиями, задаваемыми формой поперечного сечения трубы. Для трубы круглого поперечного сечения, ось которой совпадает с осью х, естественно пользоваться уравнением в цилиндрической системе координат (5.49).

Предполагая, что поток обладает осевой симметрией

,

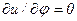получим уравнение (5.49) в виде

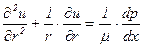(5.50)

Так как

,

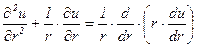то уравнение (5.50) окончательно примет следующий вид

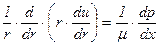. (5.51)

После последовательного двойного интегрирования получим общее решение уравнения (5.51)

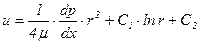. (5.52)

Произвольные постоянные и 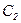определяются из граничных условий. Для круглой трубы с радиусом 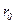они могут быть записаны так: при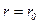 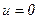, а при r = 0 u - конечная величина.

Подставив r = 0 в уравнение (5.52), получим при 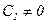бесконечное значение скорости на оси. Следовательно, для удовлетворения второго граничного условия необходимо положить .

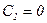Используя первое граничное условие, найдем

.

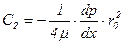Таким образом, для круглой трубы распределение скоростей по сечению будет параболическим, т.е.

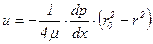. (5.53)

По уравнению (5.47) можно написать

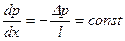, (5.54)

где 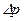- перепад давления в трубе длиной l.

Определим среднюю расходную и максимальную скорости в круглой трубе. Объемный расход Q

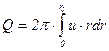(5.55)

или, подставляя u из формулы (5.53) и используя выражение (5.54), получим

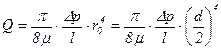. (5.56)

Формула (5.56) выражает известный закон о том, что секундный объемный расход жидкости при установившемся ламинарном движении несжимаемой жидкости в цилиндрической трубе круглого сечения пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса (или диаметра). Этот закон часто называется законом Пуазей-ля, исследовавшего законы движения крови по капиллярным сосудам.

Величина средней расходной скорости 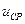, будет

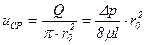. (5.57)

Наибольшее значение скорости 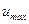, как видно из выражения (5.53), будет на оси трубы, т.е. при r = 0, и равно

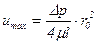. (5.58)

Из сравнения двух последних формул получим очень важное свойство ламинарного установившегося движения жидкости в круглой трубе: максимальная скорость на оси трубы в два раза больше средней расходной скорости, т.е.

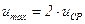. (5.59)

Это свойство можно использовать при нахождении объемного расхода, определяя не весь профиль скоростей, что необходимо в соответствии с формулой (5.55), а лишь значение скорости на оси трубы. Тогда формула для расхода будет

.

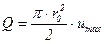Если отнести значение скорости в любой точке к максимальной скорости на оси трубы, то можно вместо выражения (5.53) получить безразмерный профиль скоростей

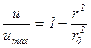(5.60)

в виде параболоида вращения с меридианальным сечением в форме параболы.

Найдем величину сопротивления при движении жидкости в трубе. Для установившегося движения в цилиндрических трубах сопротивление на данном участке определяется перепадом давления на этом участке либо по формуле

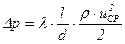, (5.61)

либо по формуле

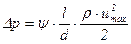, (5.62)

где 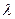и 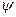- коэффициенты сопротивления.

Приравнивая правые части равенств (5.61) и (5.62) и имея в виду, что 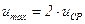, получим отношение между коэффициентам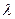и и 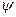в форме

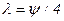. (5.63)

Определяя 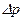из формулы (5.57) и приравнивая полученное значение правой части (5.61), найдем

,

откуда следует, что величина коэффициента сопротивления Л

, (5.64)

где 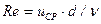- число Рейнольдса, составленное по расходной скорости 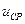и диаметру трубы d.

Выражение коэффициентов сопротивления как функций числа Рейнольдса или 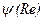называется законом сопротивления ламинарного движения вязкой жидкости в цилиндрической трубе. Зная 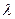или 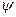, легко найти перепад давления по выражениям (5.61) и (5.62), а следовательно, и величину мощности, необходимой для перекачки заданного расхода Q (м³ / с). Формула мощности имеет вид

.

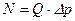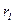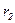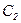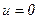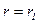Для решения задачи о продольном движении жидкости между двумя соосными цилиндрами с радиусами и постоянные и в уравнении (5.52) определим, исходя из следующих граничных условий: величина скорости на стенках цилиндров равна нулю, т.е. при и .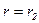

Тогда, считая 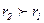получим формулу распределения скоростей

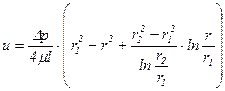. (5.65)

Величину расхода и средней скорости найдем в виде

;

,

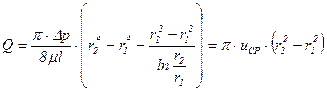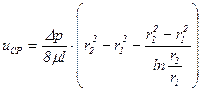откуда величина перепада давления 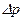будет

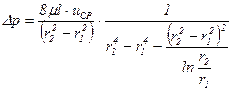. (5.66)

Для очень узких кольцевых щелей, т.е. при малой разности радиусов, допустимо щель считать ограниченной параллельными плоскостями. Тогда формула (5.66) значительно упрощается и принимает вид, очень удобный для практических расчетов

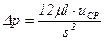, (5.67)

где 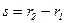- ширина щели.

Принимая для потока между соосными трубами выражение перепада давления по формуле

,

получим из выражения (5.67) закон сопротивления для ламинарного движения в щели между соосными цилиндрами

,

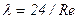где .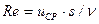

Существует также точное решение для щели, образованной не концентрическими цилиндрами. Не рассматривая здесь довольно громоздких решений, приведем лишь приближенную формулу для сопротивления при цилиндрах с мало отличающимися радиусами

,

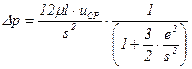где e - эксцентриситет;

s - ширина щели, которая была бы при отсутствии эксцентриситета.

Результаты многочисленных опытов при ламинарном установившемся движении в трубах круглого и кольцевого поперечного сечения хорошо совпадают с соответствующими данными, полученными по вышеприведенным формулам.

Уравнение (5.58) было решено и для труб с эллиптическим, прямоугольным и треугольным поперечными сечениями. Приведем без доказательства некоторые формулы для ламинарного стабилизованного движения в трубах эллиптического сечения.

Если а и b будут полуоси эллипса, а контур трубы в плоскости yz представить в виде 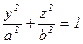, то распределение скоростей в сечении трубы

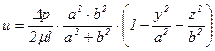(5.68)

дает уравнение поверхности эллиптического параболоида, а изотахи (линии равных скоростей) - подобные друг другу эллипсы, т.е. эллипсы с одинаковыми отношениями полуосей.

Из уравнения (5.68) видно, что скорость будет максимальной на оси трубы, т.е. при у = z = 0, и она равна

.

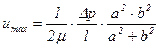Зная 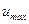можно скорость по формуле (5.68) представить в безразмерном виде

.

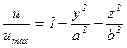Величина объемного расхода через трубу эллиптического сечения легко определяется интегрированием скорости (5.68) по сечению, т.е.

.

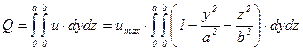После вычисления интеграла получим

.

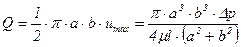Разделив объемный расход на площадь поперечного сечения трубы 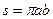, определим среднюю величину скорости

.

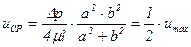Следовательно, так же как и для круглой трубы средняя скорость равна половине максимальной.

Из последней зависимости можно найти выражение для сопротивления 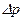и, используя выражение (5.61), получить закон сопротивления.

Легко видеть, что все формулы, полученные для трубы эллиптического сечения при а = b переходят в соответствующие зависимости для круглой трубы.

6. АБСОЛЮТНЫЙ И ОТНОСИТЕЛЬНЫЙ ПОКОЙ

(РАВНОВЕСИЕ) ЖИДКИХ СРЕД

6.1. Основная формула гидростатики

Для вывода основного уравнения гидростатики, устанавливающего зависимость давления в точке от характера действующих в жидкости массовых сил, рассмотрим равновесие элементарного прямоугольного параллелепипеда со сторонами dx, dy, dz, выделенного внутри покоящейся жидкости (рис. 6.1).

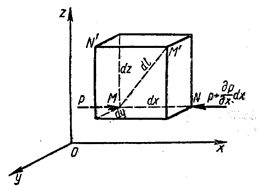
Рис. 6.1. Схема для вывода дифференциальных

уравнений равновесия жидкости

Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы, например, силы инерции переносного движения и т.п. Если сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия, которое называют относительным покоем.

В неподвижной жидкости возьмем произвольную точку М с координатами x, у и z и давлением р (рис. 6.1). Систему координат будем считать жестко связанной с сосудом, содержащим жидкость. Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz. Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила, составляющие которой, отнесенные к единице массы, равны X, Y и Z. Тогда массовые силы, действующие на выделенный объем в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объема.

Давление р есть функция координат x, y и z, но вблизи точки М по всем трем граням параллелепипеда оно одинаково, что вытекает из доказанного выше свойства гидростатического давления. При переходе от точки М, например, к точке N изменяется лишь координата x на бесконечно малую величину dx, в связи с чем функция р получает приращение, равное частному дифференциалу (др /дх) dx, поэтому давление в точке N равно
р + (др /дх) dx, где др /дх - градиент давления вблизи точки М в направлении оси x. Рассматривая давления в других соответствующих точках граней, нормальных к оси х, например в точках N' и М', видим, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину

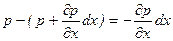. (6.1)

Ввиду этого разность сил давления, действующих на параллелепипед в направлении оси х, равна указанной величине, умноженной на площадь грани: .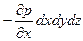

Аналогичным образом, но через градиенты давления др/ду и др/дz выразим разности сил давления, действующие на параллелепипед в направлении двух других осей.

На выделенный параллелепипед действуют лишь указанные массовые силы и силы давления, поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей запишем в следующем виде

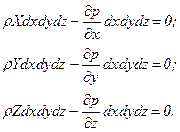(6.2)

Разделим эти уравнения на массу rdxdydz параллелепипеда и перейдем к пределу, устремляя dx, dy и dz к нулю, т.е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке М

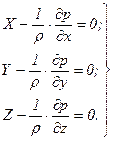(6.3)

Эта система дифференциальных уравнений гидростатики называется уравнениями равновесия Эйлера. Для практического пользования удобнее вместо приведенной системы уравнений иметь одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений на dx, второе - на dy, третье - на dz и, сложив все три уравнения, получим

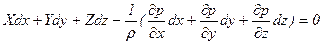. (6.4)

Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т.е. функции р (х, у, z), поэтому предыдущее уравнение можно переписать в виде

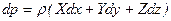. (6.5)

Полученное уравнение выражает приращение давления dp при изменении координат на dx, dy и dz в общем случае равновесия жидкости.

Рассмотрим распространенный частный случай равновесия жидкости, когда на нее действует лишь одна массовая сила - сила тяжести. Если направить ось z вертикально вверх, то Х = У = 0, Z = - g и, следовательно, для этого частного случая равновесия жидкости из дифференциальных уравнений будем иметь: dp = - rgdz. После интегрирования получим

p = - rgz + C. (6.6)

Постоянную интегрирования найдем, подставив параметры свободной поверхности, для которой (рис. 6.2) при 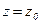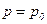, откуда 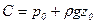. При этом

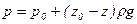или .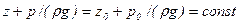

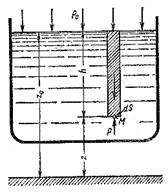
Рис. 6.2. Схема для вывода основного уравнения

гидростатики

Заменяя в предыдущем уравнении разность 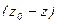на h – глубину расположения точки М, находим

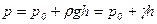. (6.7)

Полученное уравнение называют основным уравнением гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления 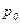на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Величина 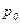является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

6.2. Определение сил давления покоящейся среды

на плоские и криволинейные стенки

В общем случае на поверхность s, погруженную в жидкость, будет действовать совокупность сил гидростатического давления, которая в соответствии с законами статики твердого тела может быть приведена к одной силе, равной главному вектору сил давления

,

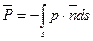и к одной паре с моментом, равным

.

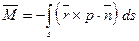Найдем величину главного вектора, приложенного к некоторой криволинейной поверхности (рис. 6.3), погруженной в жидкость.

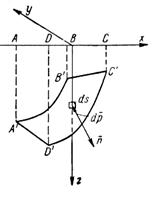
Рис. 6.3. Схема сил, воздействующих

на криволинейную поверхность

Вначале рассмотрим элементарную силу 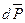, действующую на площадку ds. Очевидно, сила 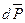будет направлена по нормали к площадке ds и равна

.

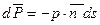Дата добавления: 2014-01-06