Проекции углов, проекция прямого угла

Фронтальная плоскость уровня - плоскость, параллельная V;

Б. Плоскости уровня

Среди проецирующих плоскостей важную роль играют плоскости уровня. Плоскость, параллельная какой-либо плоскости проекций, называется плос­костью уровня (рис. 3.13):

1) горизонтальная плоскость уровня -плоскость, параллельная Н;

3)профильная плоскость уровня - плоскость, параллельная W.

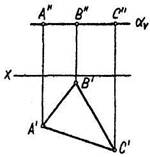
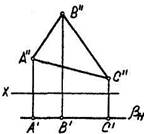
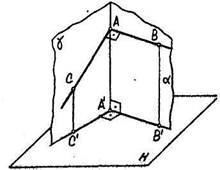
Рис. 3.13

Являясь частным случаем проецирующих плоскостей, плоскости уровня обладают их «собирательным» свойством, так, например, горизонтальная плос­кость уровня является фронтально-проецирующей olLV, поэтому проецируется на плоскость V в виде своего следа av, параллельного оси х (рис. 3.13, а).

Аналогично, фронтальная плоскость уровня Р перпендикулярна плоскости Я и проецируется на нее в виде следа р н. параллельного оси х (рис. 3.13,6).

При проецировании величина произвольного угла искажается. Произволь­ный плоский угол проецируется в натуральную величину, если он лежит в плос­кости уровня. Однако известно, что прямой угол проецируется в прямой не только тогда, когда его плоскость параллельна плоскости проекций. Сформулируем и до­кажем теорему.

Теорема. Для того чтобы прямой угол проецировался ортогонально в виде прямого угла, необходимо и достаточно, чтобы по крайней мере, одна его сто­рона была параллельна плоскости проекций, а вторая не перпендикулярна к по­следней.

Допустим, что сторона АВ пря­мого угла ВАС параллельна плоскости Я(рис. 3.14).

Спроецируем угол на Я. При этом лу­чи АА' I Я, ССХН, BB'IH.

Докажем, что угол В'АХ2' - пря-, мой.

По условию теоремы АВ парал­лельна Я. Кроме того, АВ и ее проек­ция А В' лежат в одной проецирующей плоскости а. Из этого следует, что АВ || АЪ'.

Рис. 3.14

Далее известно, что АА' L Н, значит АА' 1АЪ', прямые АВ нАЪ' - парал­лельны, значит АВ 1 АА'.

Таким образом, прямая АВ X АА' и АВ 1 АС, т. е. она перпендикулярна к двум прямым плоскости у, значит она перпендикулярна плоскости у. Но тогда А Ъ' как параллельная АВ, также перпендикулярна плоскости у, а значит она перпен­дикулярна к любой прямой этой плоскости, в частности, ЛВ'А'С- прямой, т. е. теорема доказана.

Применяя полученные выводы к проекциям на комплексном чертеже можно сформулировать такие условия: две взаимно перпендикулярные прямые тогда и только тогда сохраняют перпендикулярность на горизонтальной проекции, когда, по крайней мере, одна из них горизонталь.

Аналогично, эти условия можно записать для фронтальной и профильной проекций (рис. 3.15).

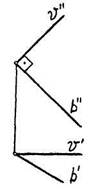
Рис. 3.15

Дата добавления: 2014-01-07