Линию наибольшего наклона, перпендикулярную к горизонтали, называют также линией наибольшего ската

Линиями наибольшего наклона называются прямые, принадлежащие плоскости и перпендикулярные к ее линиям уровня.

Линии наибольшего наклона

Среди прямых плоскости следует отметить еще замечательные прямые, ксь торые тоже относят к главным - это прямые, образующие с плоскостями проек­ций наибольшие углы. Их называют линиями наибольшего наклона к плоскостям проекций.

С помощью построения этих линий решается задача определения углов на­клона плоскости к плоскостям проекций, т. е. двугранных углов между плоско­стью и плоскостями проекций.

Как известно из стереометрии, двугранный угол измеряется своим линей­ным углом, т. е. углом, образованным прямыми, перпендикулярными к ребру дву­гранного угла. Значит, двугранный угол между плоскостью и плоскостью проек ций — это угол между линией наибольшего наклона и ее проекцией на эту плос­кость.

Теорема. Прямые плоскости, перпендикулярные к ее линиям уровня, явля­ются пиниями наибольшего наклона.

В плоскости общего положения р, пересекающей Н по следу р„, проводим пря­мую АВ, перпендикулярную к горизонтали h (ABxh) (рис. 3.16). Необходимо до­казать, что угол наклона прямой АВ к плоскости Я- наибольший но сравнению с углом, образуемым любой другой прямой, например А С.

Угол между прямой АВ и плоско­стью Н - это угол между АВ и ее проек­цией на плоскость Н. Проведем А А' перпендикулярно Н, угол АВ'А' = <р -искомый угол.

Докажем, что <р > i|/ - угла между лю­бой другой прямой АС в плоскости (3 и плоскостью Н.

АВ'х Рн, следу плоскости р, так как
h |j р_н, а АВ'Х h. Значит А С" больше
АВ', так как АВ' - перпендикуляр к рн, а
^Рис-^Зл6 АС- наклонная.

⁴ Рассмотрим два прямоугольных треугольника &.ААЪ'н &АА'С'~ с общим катетом АА'. Вращая &ААЪ'- вокруг АА' до совпадения с аАА'С, совмещаем плоскости рассматриваемых треугольников. Тогда, так как АВ меньше АС, угол ABi'А'=(р больше угла АС'А'= \у - как внешний угол треугольника АС'В/. Итак, доказали, что ср > у, т. е. линия АВ, перпендикулярная к горизонтали, дей­ствительно линия наибольшего наклона к горизонтальной плоскости проекций //. Отметим еще, что проекция линии наибольшего наклона АЪ' X h', и А И' X рн на основании теоремы о проецировании прямого угла, т. е. горизонтальная проекция линии наибольшего наклона к плоскости Н перпендикулярна к горизон-шальной проекции горизонтали.

Аналогичные доказательства можно провести для линий наибольшего на­клона плоскости к плоскостям проекций VhW.

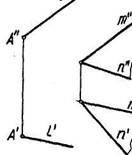
Пример: построить траекторию движения дождевой капли (точки А), скаты­вающейся по плоскости параллельных прямых (а|(Ь)(рис. 3.17).

Построение следует начать с построения горизонтали h(h", h') в плоскости а(а || Ь), Затем, зная, что горизонтальная проекция линии наибольшего ската пер­пендикулярна к горизонтальной проекции горизонтали, строим АЪ' X h', затем по линии связи определяем В" е b", A" e а". Искомая траектория найдена - это AB{AW,A"B").

Для того, чтобы определить угол наклона плоскости а(а \ I b) к плоскости Н, необходимо определить натураль­ную величину отрезка АВ линии ската, построив прямоугольный треугольник на ее горизонтальной проекции АЪ', взяв в качестве второго катета раз­ность высот точек А и В. Искомый угол q> —угол между линией ската А Ъ* и ее горизонтальной проекцией А Ъ'.

Рис. 3.17

3.2.7. Параллельность прямой и плоскости, двух плоскостей

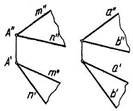
Построение прямой, параллельной данной плоскости основано на известном положении стереометрии: прямая параллельна плоскости, если она параллельна нюбой прямой, лежащей в этой плоскости.

Чтобы построить на эпюре пря­мую /, параллельную плоскости а (тпп) и проходящую через точку А, достаточно построить ее так, чтобы она была параллельна любой прямой, при­надлежащей этой плоскости. Например: /1| т (/' || т', Г || т"). Таких прямых можно построить бесчисленное множество.

Две плоскости параллельны, если две пересекающиеся прямые одной плос­кости соответственно параллельны двум пересекающимся прямым второй плос­кости.

Поэтому, чтобы задать на эпюре плос­кость a (mnn), проходящую через точку А и параллельную плоскости Р (anb), доста­точно построить проекции пересекающихся прямых тип, соответственно параллель­ных прямым а и в (т || а, п || Ъ).

Рис. 3.19

3.3. Линейчатые поверхности

Определение. Линейчатой поверхностью называется поверхность, кото­рая может быть образована движением прямой линии в пространстве.

В зависимости от закона перемещения образующей получаются различные типы линейчатых поверхностей.

3.3.1. Линейчатые поверхности с одной направляющей (торсы) А. Коническая и пирамидальная поверхности

Коническая поверхность образуется прямой линией а (образующей), которая скользит по кривой линии т (направляющей), имея при этом неподвижную точку S (вершину).

Определитель конической поверхности состоит из вершины S и направляю­щей кривой т. т. е. Ф (т, S)\A] (рис. 3.20, а).

а б

Рис. 3.20

Задание на чертеже с помощью определителя приведено на рис. 3.20, б. Каркас поверхности может быть составлен из набора прямолинейных образую­щих. Точку N на поверхности строят при помощи образующей а, проходящей че­рез вершину S и точку 1, принадлежащую направляющей т.

Если направляющей поверхности служит ломаная линия, состоящая из пря­молинейных звеньев, то коническая поверхность превратится в пирамидальную поверхность.

Б. Цилиндрическая поверхность и призматическая

Цилиндрическая поверхность образуется прямой линией а, которая скользит по кривой линии т (направляющей), оставаясь параллельной самой себе

5>(рис. 3.2U

Цилиндрическую поверхность можно рассматривать как частный слу­чай конической поверхности, верщина которой удалена в бесконечность, и, следовательно, образующие параллель­ны друг другу (пересекаются в беско­нечно удаленной точке).

Определитель цилиндрической поверхности состоит из направляющей кривой т и образующей а: Ф (а, т)[А\. На рис. 3.21 приведено задание на чер­теже элементами определителя. Точка A{A'^i") построена на поверхности Ф при помощи образующей a_t, инцидент­ной поверхности, так как она проходит через точку 1, принадлежащую направ­ляющей т и параллельна заданной об­разующей а. Рис. 3.21

Если направляющей поверхности служит ломаная линия, то цилиндриче­ская поверхность превращается в призматическую.

Если направляющей цилиндрической и конической поверхности является кривая 2-го порядка, т. е. эллипс (окружность), гипербола, парабола, то образуется коническая или цилиндрическая поверхность 2-го порядка. Подробнее на них ос­тановимся при рассмотрении поверхностей вращения.

В. Поверхность с ребром возврата (торс)

Поверхностью сребром возврата (торсом), называется поверхность, об­разованная перемещением прямолинейной образующей а, касающейся во всех сво­их положениях некоторой пространственной кривой т, называемой ребром воз­врата.

Дата добавления: 2014-01-07