На прошлой лекции мы записали УМ совместно с простейшими МУ в виде

Симметризованные уравнения Максвелла.

ЛЕКЦИЯ 2

Симметризованные уравнения Максвелла. Принцип перестановочной инвариантности. Уравнения Максвелла в монохроматических полях. Уравнения Гельмгольца для электрического и магнитного полей. Уравнения для векторов Фарадея.

УМ 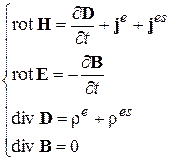, МУ 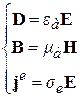. (2-1)

Напомню, что индекс “e” означает, что речь идет об электрических зарядах и токах, а индексом “ a ” отмечены сторонние заряды и токи.

Из такой записи видно, что система УМ несимметрична из-за отсутствия магнитных зарядов и токов. Сделаем ее, пока формально, более симметричной, введя магнитные заряды и токи. На микроуровне это не имеет физического смысла, но на макроуровне введение магнитных зарядов и токов имеет физический смысл и, как мы увидим в дальнейшем, существенно упрощает анализ электромагнитных полей. Аналогично введем в УМ и сторонние магнитные заряды и токи.

После введения магнитных зарядов и токов система УМ и МУ примет следующую симметричную форму

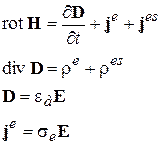, (2-2)

Здесь в правом столбце мы ввели магнитные и сторонние магнитные заряды и токи, а также материальные уравнения, связывающие магнитный ток с магнитным полем через магнитную объемную проводимость среды σ _m.

Приведенная нами симметризация УМ и МУ весьма полезна. Система УМ в форме (2-2) обладает свойством перестановочной инвариантности (перестановочной двойственности).

Принцип перестановочной инвариантности.

Сделаем в УМ и МУ замену

E Û H, D Û -B, j ^e Û - j ^m, e _a Û -m _a, r ^e Û - r ^m _, s _e Û- s _m, (2-3)

аналогичная замена используется для сторонних токов и зарядов.

Здесь стрелка в соотношениях вида E Û H означает, что величина, к которой направлена стрелка, заменяется на величину, стоящую по другую сторону стрелки.

Возьмем левый столбец в системе (2-2) и заменим входящие в него величины в соответствии с (2-3). Видим, что левый столбец перешел в правый. Аналогично, подставляя в правый столбец УМ (2-2) соотношения (2-3) получим левый столбец УМ. Таким образом, подстановка (2-3) переводит УМ сами в себя.

Но сила принципа перестановочной инвариантности в том, что он может быть применен не только к УМ, но и к решениям УМ.

Напомним, что система (2-2) является линейной и к ней применим принцип суперпозиции. Это означает, в частности, что общее решение неоднородных (содержащих сторонние заряды и токи) УМ может быть представлено в виде суммы решений 2-х неоднородных УМ: одно из них определяется сторонними электрическими токами, а второе - сторонними магнитными токами.

Предположим теперь, что мы решили задачу излучения э/м волн сторонними электрическими токами и нам требуется решить задачу излучения э/м волн сторонними магнитными токами, зависящими от пространственной и временной переменных точно так же, как и сторонние электрические токи. Тогда решение задачи об излучении сторонних магнитных токов может быть получено из решения задачи об излучении сторонних электрических токов путем применения к последнему решению подстановки (2-3).

Таким образом, принцип перестановочной инвариантности позволяет получать из одного решения УМ заменой (2-3) другое решение без дополнительной аналитической работы.

Замечание 1. Существует несколько форм принципа перестановочной инвариантности (см. [1, 2,3]). Приведенная нами форма соответствует учебникам [1,2]. В книге [3] приведена другая форма принципа перестановочной инвариантности. Вы может сами предложить другие варианты. Принцип перестановочной инвариантности применим и к негармоническим полям, и к гармоническим.

Замечание 2. Систему (2-2) можно рассматривать как совокупность постулатов теории электромагнетизма для материальных сред. Можно ли считать, что этих постулатов достаточно для анализа э/м полей?

И. Е. Тамм ([4] гл. 7, § 91) указывает, что УМ должны быть дополнены постулатом об энергии э/м поля, лишь в этом случае совокупность УМ станет доступной проверке на опыте. Энергетические соотношения в электродинамике мы рассмотрим на отдельной лекции.

Дата добавления: 2014-01-07