Уравнения Максвелла для монохроматических полей

Электромагнитные поля, определяемые УМ (2-2), являются функциями трех пространственных координат и времени. Можно упростить анализ э/м полей, перейдя от нестационарных полей к их спектральным представлениям. Напомню, (см. [5], гл. 2), что любой сигнал U (t) может быть представлен интегралом от спектральной плотности сигнала 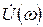. Сигнал U (t) и его спектральная плотность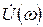связаны прямым и обратным преобразованиями Фурье

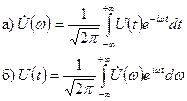(2-4)

Отметим, что спектральная плотность 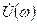в общем случае комплекснозначная функция частоты .

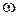Представление (2-4б) можно трактовать, как представление произвольного сигнала в виде суммы монохроматических (гармонических) колебаний.

Рассмотрим вещественную гармоническую функцию

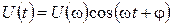(2-5)

Здесь 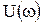- амплитуда, 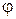- фаза гармонического колебания круговой частоты 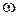=2π f.

Представим U (t) в виде

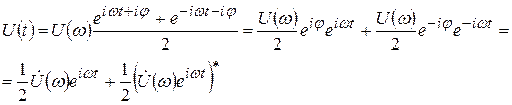
Здесь 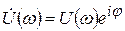, звездочка *- означает знак комплексного сопряжения. Комплексное число 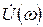будем называть комплексной амплитудой.

Пусть нам известна комплексная амплитуда 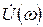. Тогда можно найти соответствующую ей вещественную функцию времени 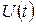по правилу

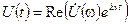(2-6)

Действительно

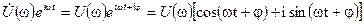
Из последнего соотношения следует, что

.

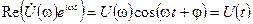Рассмотрим теперь векторное поле. Пусть V (r, t) - вещественная векторная функция, описывающая монохроматическое поле частоты 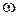. Запишем вектор V (r, t)в декартовой системе координат

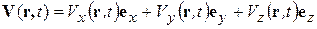
Здесь 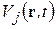- компоненты вектора V, 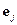- единичные векторы, j=x,y,z

В случае гармонических колебаний

.

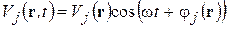К векторным монохроматическим полям также можно применить определение комплексных амплитуд. Обозначим

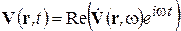(2-7)

Здесь 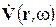- вектор комплексной амплитуды монохроматического поля V (r, t)

Функция V (r, t)может быть записана в виде

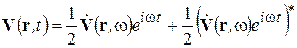
Звездочка над вторым слагаемым означает комплексное сопряжение. Часто используют запись

,

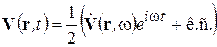обозначение 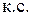- это комплексно сопряженная по отношению к 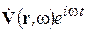величина.

Аналогично (2-4) преобразование Фурье можно применить к нестационарным УМ (2-2).

При этом, применив прямое преобразование Фурье вида (2-4а) к УМ (2-2), мы получим УМ для спектральных плотностей и тем самым сократим число независимых переменных (т.к. спектральные плотности полей зависят только от r, а от времени не зависят).

Вместо применения преобразования Фурье к УМ проще воспользоваться методом комплексных амплитуд.

Согласно этому методу исходные УМ для вещественных монохроматических полей частоты 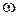с учетом связи

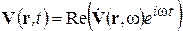
переводятся в УМ для комплексных амплитуд подстановкой вместо векторных и скалярных функций V (r, t) и V_j (r, t) величины , .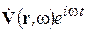

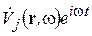Нестационарные УМ вида (2-2) при этом существенно упрощаются, так как дифференцирование по времени монохроматических полей дает

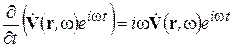
т.е. оператор 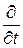заменяется в УМ на 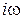. Перейти к вещественным представлениям исходных немонохроматических полей можно с помощью обратного преобразования Фурье вида (2-4б).

Выведем УМ для комплексных амплитуд. Подставим в исходные УМ (2-2) вместо вещественных векторных полей E (r, t), H (r, t) и т.д. комплексные величины 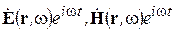и т.д., то же сделаем для скалярных величин ρ ^e, ρ ^m. После дифференцирования по t и исключения общего множителя 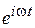получаем (сторонние токи и заряды, а также точки над комплексными амплитудами для упрощения опускаем)

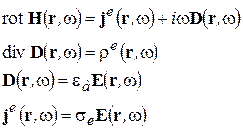
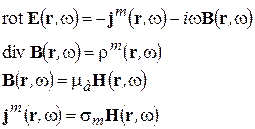(2-8)

Подставим МУ в УМ. Получим для первых уравнений в (2.8)

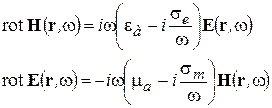(2-9)

Преобразуем теперь уравнение

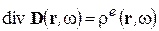. (2-10)

Учтем, что ток и заряд связаны уравнением непрерывности

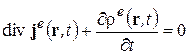. (2-11)

Переходя к комплексным амплитудам, получим из (2-11)

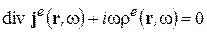. (2-12)

Далее исключаем с помощью (2-12) плотность заряда из (2-10) и затем исключаем ток и электрическую индукцию с помощью материальных уравнений в (2-8). В результате получим

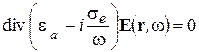. (2-13)

Аналогично уравнение 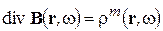перейдет в уравнение

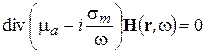. (2-14)

Сопоставляя (2-9), (2-13), (2-14) видим, что мы можем ввести новые диэлектрическую и магнитную проницаемости

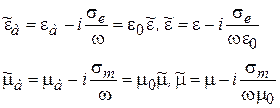(2-15)

В (2-15) 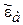,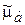- абсолютные комплексные диэлектрическая и магнитная проницаемости среды, 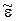,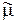- относительные комплексные диэлектрическая и магнитная проницаемости среды.

С учетом (2-15) система УМ и МУ сводится к виду

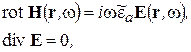
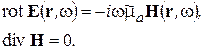(2-16)

Система (2-16) является максимально простой формой УМ для комплексных амплитуд. Подчеркнем, что в системе (2-16) уравнение 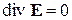является следствие 1-го УМ, а уравнение 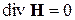- следствием 2-го УА. Это легко показать, действуя оператором div на первые два уравнения Максвелла. Поэтому фактически мы свели систему однородных УМ для гармонических полей всего к двум уравнениям

Возможно и другое представление системы УМ, которое окажется более удобным при анализе сопряжения полей на границах раздела сред (этот вопрос будет изучаться позднее).

Введем новые векторы комплексных амплитуд электрической и магнитной индукции, определив их следующим образом

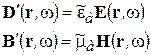, (2-17)

тогда в соответствии с (2-9), (2-13), (2-14) система УМ сводится к виду

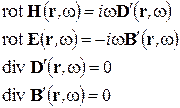(2-18)

Напомним теперь, что мы при переходе от УМ для мгновенных значений полей к УМ для комплексных амплитуд рассматривали УМ без сторонних зарядов и токов. Если оставить в исходных УМ сторонние заряды и токи, то мы получим следующие УМ для комплексных амплитуд, являющиеся обобщением (2-18)

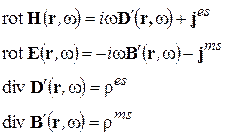(2-19)

Если в (2.19) заменить векторы электрической и магнитной индукции в соответствии с (2.17), то придем к системе неоднородных УМ в форме

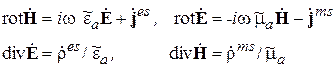(2.20)

Таким образом, перейдя к монохроматическим полям, мы получили весьма компактные УМ для комплексных амплитуд полей в формах (2-16), (2-18), (2-19), (2-20).

Следует сделать несколько замечаний по поводу полученных уравнений.

Замечание 3

Материальные уравнения (2-15) получены в результате перехода к комплексным амплитудам в простейших МУ (см. систему (2-2)). При этом 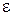, , 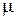, 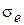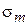в (2-16) не зависят от частоты. Однако МУ (2-15) сохраняют вид и для сред с частотной дисперсией, когда 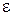, , 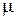, 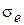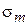являются функциями частоты. МУ вида (2-15) в этом случае получают из МУ сред с временной дисперсией после применения прямого преобразования Фурье.

Замечание 4

Связь вещественных монохроматических полей с комплексными амплитудами мы определяли соотношением

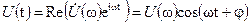
Иногда определяют связь вещественного поля с комплексной амплитудой заменой

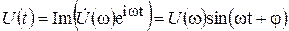
Очевидно, что такое определение отличается от предыдущего только сдвигом по фазе на 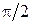(по времени - на четверть периода), что непринципиально и соответствует просто сдвигу отсчета по времени.

Замечание 5

В определении монохроматического поля

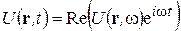
функция 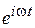называется временным множителем. Использование временного множителя 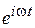соответствует паре преобразований Фурье (2-5).

Однако можно определить связь вещественного поля с комплексной амплитудой соотношением

.

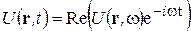Замена временного множителя 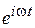на 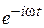приводит к тому, что УМ и МУ для комплексных амплитуд, найденных с временным множителем 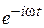, оказываются комплексно сопряженными по отношению к УМ и МУ для комплексных амплитуд, найденных с временным множителем 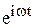. Например:

для временного множителя 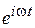для временного множителя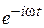

1-е УМ: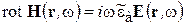

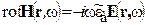
диэлектрическая проницаемость

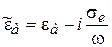
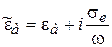
Отметим, что при таких определениях для поглощающих сред 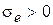независимо от вида временного множителя.

В физической литературе принято использовать временной множитель 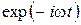, в технической - множитель 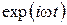. Обращайте на это внимание при чтении книг и статей. Есть книги, где в разных главах использованы различные временные множители.

Бывают ошибки такого рода: автор работает с системой УМ с временным множителем 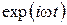, но берет для среды с потерями представление 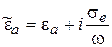, и 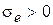. При этом поле не затухает в среде вследствие потерь, а возникает растущее поле, т.е. физически противоположный затуханию эффект (активная среда).

Дата добавления: 2014-01-07