Векторные уравнения Гельмгольца для электрического и магнитного полей

Выше мы получили УМ для монохроматических полей в форме (2.20). Система (2.20) определяет 2 неизвестных поля: Е и Н. Можно еще дальше пойти по пути упрощения уравнений. Например, исключить из (2.20) Н либо Е, а также сторонние заряды, тогда вместо системы (2.20) получим одно уравнение относительно Е либо Н. В итоге получим уравнения, которые называются уравнениями Гельмгольца (УГ). В англоязычной литературе их принято называть приведенными волновыми уравнениями. Выводом этих уравнений мы и займемся.

Нам предстоит много технической работы по преобразованию уравнений. Чтобы упростить работу, опустим в дальнейшем точки над величинами, обозначающими комплексные амплитуды, и тильды над величинами e _а и m _а.

Выведем УГ для поля Е. Для этого из первого УМ в (2.20) необходимо исключить Н. Применим операцию rot ко 2-му УМ.

.

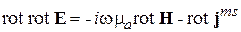Далее исключим rot Н с помощью 1-го УМ.

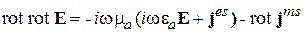
Теперь воспользуемся формулой векторного анализа.

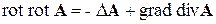. (2.21)

Здесь D – оператор Лапласа*)

Получим

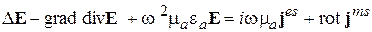(2.22)

Далее учтем 3-е УМ

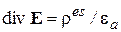
и уравнение непрерывности для сторонних токов

.

Отсюда следует, что

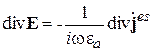
Подставив это выражение для div E в (2.22), окончательно получим

уравнение для электрического поля

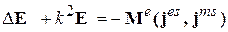, (2.23)

где k = 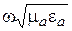- величина, называемая постоянной распространения (или волновым числом). Волновое число для среды без потерь можно записать в форме

, (2.24)

где с – скорость света а вакууме, V – скорость света в материальной среде с относительными проницаемостями ε и μ.

В правой части (2.23) стоит функция сторонних токов

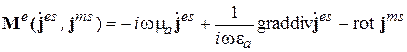. (2.25)

______

*) Действие оператора Лапласа на скалярное поле U определяется соотношением D U =div grad U. Действие оператора Лапласа на векторное поле А – соотношением (2.21). Оператор Лапласа также часто записывают через оператор «набла» в форме ÑÑ или Ѳ. В некоторых книгах обозначение D означает только действие на скалярную функцию, а в векторной форме используют соотношение Ѳ.

Уравнение (2.23) называется неоднородным векторным УГ для электрического поля, т.к. в его правой части стоит функция сторонних токов М ^e.

Аналогично можно получить УГ для магнитного поля. Для этого используем принцип двойственности, т.е. проведем замену H Þ Е, j ^ms Û- j ^es, e _a Û -m _a. В результате получим

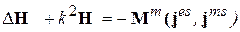, (2.26)

где

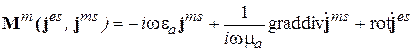. (2.27)

Заметим, что правые части уравнений (2.23) и (2.26) отличны от нуля только в объеме сторонних токов V_{s .}, т. е.

M ^e¹ 0, M ^m¹ 0,если q Î V^s,

M ^e =0, M ^m =0,если q ÏV ^s,

Здесь точки q- координаты источников, т.е. правых частей уравнений (2.23) и (2.26). В области, где M ^e =0, M ^m =0, уравнения (2.23) и (2.26) становятся однородными (правые части равны нулю).

Таким образом, вместо системы (2.20) мы получим УГ (2.23) для Е и (2.26) для Н.

Упрощение состоит в том, что мы получим одно уравнение (для Е или Н) вместо системы (2.20). Правда, уравнение более сложное – 2-го порядка в частных производных вместо системы уравнений 1-го порядка для Е и Н. Но решать одно уравнение обычно легче, чем систему.

Заметим, что для отыскания полей Е и Н нет необходимости решать оба УГ для Е и Н. Достаточно решить одно уравнение, например (2.23) для Е, а затем найти поле Н через известное поле Е с помощью 2-го УМ (2.20).

УГ для Е и Н широко используются для отыскания э/м полей в области вне источников. Однако когда речь идет об излучении источников, эти уравнения весьма неудобны, т.к. в правых частях УГ для Е и Н стоят дифференциальные операции над токами. Это может вызвать трудности. Зависимости сторонних токов от координат часто задаются из приближенных, эвристических соображений или на основе экспериментальных данных. При таком способе задания сторонних токов дифференцирование неточно заданной функции тока может существенно увеличить погрешность производных тока (по сравнению с истинными). В результате решение УГ с неточно заданной правой частью может дать ошибочный результат.

Есть очень изящный прием, позволяющий обойти эти трудности. Для этого вводят вспомогательные величины, называемые векторными потенциалами. Вопросы введения векторных потенциалов мы обсудим на следующей лекции.

Дата добавления: 2014-01-07