Общее уравнение прямой. Различные виды уравнений прямой на плоскости

Различные виды уравнений прямой на плоскости

Уравнение

Ax+By+C=0 (6.1)

с произвольными коэффициентами A, B и C такими, что A и B не равны одновременно нулю, называется общим уравнением прямой L.

Уравнение (6.1) имеет хотя бы одно решение , т.е. существует точка , координаты которой удовлетворяют уравнению (6.1):

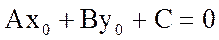(6.2)

Вычитая из уравнения (6.1) тождество (6.2), получаем уравнение

, (6.3)

эквивалентное уравнению (6.1).

Если точка 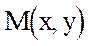лежит на прямой L, то ее координаты удовлетворяют уравнению (6.3), векторы , перпендикулярный к прямой L и перпендикулярны и их скалярное произведение

равно нулю. Если же точка не лежит на прямой L, то ее координаты не удовлетворяют уравнению (6.3).

Итак, уравнение (6.3) определяет прямую L, проходящую через точку 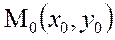и перпендикулярную вектору 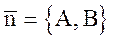. Этот вектор будем называть нормальным вектором прямой (6.1).

Замечание. Если два уравнения 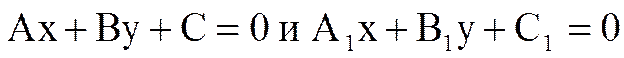определяют одну и ту же прямую, то существует такое вещественное число t, что справедливы равенства .

1.1.5.2. Уравнение прямой с угловым коэффициентом

Пусть прямая не параллельна оси Ox, тогда в уравнении (6.1) коэффициент 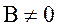. Углом наклона этой прямой к оси Ox назовем угол , образованный прямой с положительным направлением оси Ox.

Если прямая параллельна оси Ox, то угол наклона a будем считать равным нулю.

Угловым коэффициентом прямой назовем тангенс угла наклона этой прямой к оси Ox, .

Для прямой, параллельной оси Ox, угловой коэффициент равен 0, а для прямой, перпендикулярной оси Ox, угловой коэффициент не существует .

Из уравнения (6.3) и того, что- нормальный вектор прямой следует, что .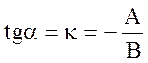

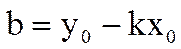Отсюда получим уравнение прямой с угловым коэффициентом в виде . Если обозначить , то последнее уравнение примет вид

(6.4)

Это уравнение и называется уравнением прямой с угловым коэффициентом. Здесь k- угловой коэффициент данной прямой, а b - отрезок, отсекаемый данной прямой на оси Oy, начиная от начала координат (при ).

Дата добавления: 2014-01-07