Взаимное положение прямых

Взаимное положение прямых и плоскостей

Две прямые в пространстве, могут занимать самые различные положения одна по отношению к другой: пересекаться, быть параллельными и в крест расположенными (скрещивающимися).

Параллельные прямые. К числу свойств параллельного проецирования относится следующее: проекции двух параллельных прямых параллельны между собой. Если прямая АВ (рис. 38) параллельна прямой CD, то проецирующие плоскости s и g параллельны между собой и при пересечении этих плоскостей с плоскостью проекций П₁ получаются параллельные между собой проекции прямых А₁В₁ и C₁D₁.

Однако в этих плоскостях могут быть расположены прямые, для которых А₁В₁ и C₁D₁ будут являться проекциями, но сами эти прямые не будут параллельны между собой. Например, прямая А₀В₀ не параллельна прямой C₀D₀.

Из указанного свойства параллельного проецирования следует, что горизонтальные, фронтальные и профильные проекции параллельных прямых будут параллельны между собой. Следовательно, если даны параллельные между собой проекции на всех трех плоскостях проекций, то это утверждение справедливо для всех прямых. Отсюда можно сделать вывод, что если одноименные проекции двух прямых попарно параллельны, то прямые в пространстве тоже параллельны. Однако, если даны параллельные между собой проекции прямых лишь на двух плоскостях проекций, то это утверждение справедливо только для прямых общего положения и может не подтвердиться для прямых уровня (прямых параллельных одной из плоскостей проекций).

На рис. 39 даны профильные прямые AС и ВМ. Хотя на двух плоскостях проекций (фронтальной и горизонтальной) их проекции параллельны, по профильным проекциям видно, что эти прямые не параллельны между собой.

То, что данные прямые не параллельны между собой можно определить, не прибегая к построению третьей проекции: достаточно обратить внимание на чередование буквенных обозначений. На фронтальной проекции прямой АС дальше от оси х располагается проекция точки А, на горизонтальной проекции дальше от оси х – проекция точки С. У прямой ВМ буквенные обозначения точек расположены в другой последовательности: на фронтальной и горизонтальной проекциях дальше от оси х расположена проекция одной и той же точки В. Этот признак означает, что прямые АС и ВМ в пространстве расположены в разных направлениях, что и подтверждается при построении профильных проекций данных прямых. Для параллельных прямых должно быть одинаковым расположение буквенных обозначений точек и длина проекций прямых на каждой плоскости проекций должна изменяться пропорционально.

Если через данную точку А на рис. 40 требуется провести прямую b, параллельную данной прямой с, то построение сводится к проведению через проекцию А₁ прямой, параллельной c₁, и через проекцию А₂ прямой, параллельной c₂. В случае если параллельные прямые расположены в общей для них проецирующей плоскости (рис. 41), перпендикулярной, например, к П₂, то фронтальные проекции таких прямых будут расположены на одной линии и совпадать со следом проецирующей плоскости на П₂.

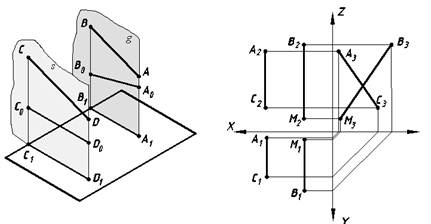
Рис. 38 Рис. 39

Рис. 40 Рис. 41

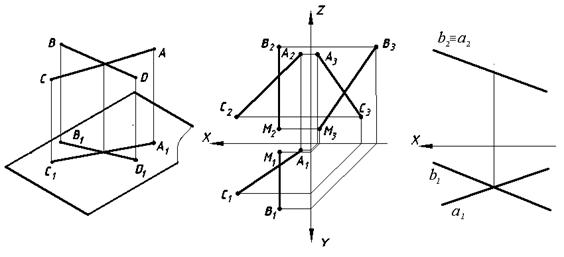
Рис. 42 Рис. 43 Рис. 44

Прямые линии, имеющие общую точку, называются пересекающимися. Одноименные проекции этих прямых тоже пересекаются, и точки их пересечения являются проекциями одной точки пространства, т. е. принадлежат одной линии связи.

Действительно (рис. 42), если точка пересечения принадлежит обеим прямым, то проекция этой точки должна быть точкой пересечения проекций данных прямых. Данное утверждение справедливо для всех прямых общего положения. Но если одна из прямых является прямой уровня, то о пересечении прямых можно судить только тогда, когда даны проекции этой прямой на плоскости ей параллельной. Например, в случае на рис. 43 прямые АС и MВ, из которых прямая MВ параллельна плоскости П₃, не пересекаются между собой, это может быть подтверждено построением профильных проекций.

Изображенные на рис. 44 пересекающиеся прямые расположены в общей для них плоскости, перпендикулярной к П₂. Поэтому фронтальные проекции этих прямых расположены на одной прямой.

Прямые, не пересекающиеся и не параллельные между собой, называют вкрест расположенными или скрещивающимися (рис. 45). Хотя одноименные проекции и пересекаются между собой, точки их пресечения не могут быть соединены одной линией связи. Точка пересечения таких прямых является проекцией двух точек, одна из которых принадлежит первой прямой, а вторая – другой прямой. Эти точки называют конкурирующими (см. параграф 2. 2). Например, на рис. 46 точка К с проекциями К₁ и К₂ принадлежит прямой a, точка L с проекциями L₁ и L₂ принадлежит прямой b. Эти точки одинаково удалены от плоскости проекций П₂, но расстояния их от плоскости П₁ различны: точка L располагается дальше от П₁, поскольку ее фронтальная проекция L₂ располагается выше фронтальной проекции точки К–К₂.

Точки Р и F одинаково удалены от плоскости П ₁, но расстояния этих точек от плоскости П ₂ различны. Горизонтальная проекция точки Р – Р ₁ располагается ниже горизонтальной проекции точки F – F ₁, следовательно точка Р находится в пространстве ближе к наблюдателю и дальше от П ₂, чем точка F.

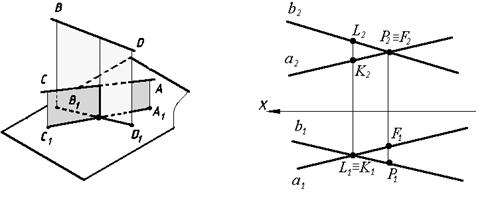
Рис. 45 Рис. 46

Дата добавления: 2014-01-07