Взаимное положение прямой и плоскости

Прямая линия может принадлежать плоскости, пересекать ее и быть ей параллельна.

Прямая линия принадлежит плоскости, если:

а) она проходит через две точки, принадлежащие плоскости;

б) она проходит через одну точку плоскости, параллельно любой прямой этой плоскости.

Данный случай взаимного положения прямой и плоскости был рассмотрен в главе 5.

Построение прямой, параллельной заданной плоскости, основан на следующем положении, известном из геометрии: прямая параллельна плоскости, если она параллельна любой прямой в этой плоскости.

Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие. Например, через точку Н (рис. 47) требуется провести прямую, параллельную плоскости, заданной треугольником АВС и одновременно параллельной П₁. Если прямая параллельна П₁, то ее фронтальная проекция будет параллельна оси Х и сама прямая в таком положении будет являться горизонтальной прямой уровня. Для решения задачи и выполнения заданных условий проводим прямую, принадлежащую треугольнику АВС и параллельную П₁, затем определяем горизонтальную проекцию этой линии.

Через фронтальную проекцию точки Н – Н₂ проводим прямую, параллельную П₁, а через горизонтальную проекцию точки Н – Н₁, проводим прямую, параллельную построенной прямой на горизонтальной проекции треугольника АВС.

Рис. 47

Если необходимо установить, параллельна ли некоторая прямая заданной плоскости, можно попытаться провести в этой плоскости прямую, параллельную заданной прямой. Если это условие выполнить не удается, то можно сделать вывод, что прямая и плоскость не параллельны между собой.

Очевидно, если прямая пересекает плоскость, она имеет с ней общую точку, при этом и прямая, и плоскость могут занимать в пространстве любое положение. Задача на пересечение прямой и плоскости общего положения является классической позиционной задачей начертательной геометрии. Решается она по определенной схеме, которая используется для задач:

на определение точек пересечения прямых с поверхностью;

линий пересечения плоскости с поверхностью;

линий пересечения любых поверхностей с линейчатыми поверхностями и др.

В решении каждой задачи используют проецирующую плоскость как секущую вспомогательную плоскость.

Свойство проецирующих плоскостей, которое позволяет их использовать в качестве вспомогательных, заключается в следующем: любая фигура, принадлежащая проецирующей плоскости, имеет одну из проекций на соответствующем следе этой плоскости. Например, на рис. 48 прямая а пересекается с фронтально проецирующей плоскостью S.

Рис. 48

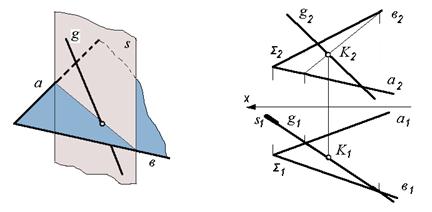
Рис. 49

На фронтальном следе плоскости S₂ находим сначала фронтальную проекцию точки пресечения прямой и плоскости - 1₂, затем горизонтальную проекцию определяем как недостающую проекцию точки, принадлежащую прямой а – 1₁.

Рассмотрим схему решения задачи, если плоскость и прямая занимают произвольное положение в пространстве. На рис.49 дана плоскость S, заданная пересекающимися прямыми а и в, и прямая g.

Последовательность решения задачи:

1) через прямую g проводим вспомогательную секущую горизонтально-проецирующую плоскость s, которая отображается на горизонтальную плоскость проекций в виде прямой линии, совпадающей с горизонтальной проекцией линии g;

2) определяем линию пересечения проецирующей плоскости s с заданной плоскостью S на обеих плоскостях проекций;

3) определяем точку К пересечения данной прямой g с линией пересечения плоскостей s и S, сначала на горизонтальном следе плоскости, затем при помощи линии связи на фронтальной плоскости проекций. Точка К– общая для прямой g и плоскости s и является искомой точкой пересечения прямой g и плоскости S;

4) методом конкурирующих точек определяем видимость участков прямой относительно плоскости.

Сравнивая положения проекций фронтально-конкурирующих точек 1 и 2, можно заметить, что горизонтальная проекция точки 1 – 1₁ располагается ниже горизонтальной проекции точки 2–2₁, следовательно, на фронтальной плоскости проекций точка 1 будет видима. Поскольку точка 1 принадлежит прямой g, можно сделать вывод о том, что на фронтальной проекции участок прямой g до точки пересечения К будет видимым.

На горизонтальной плоскости проекций определяем видимость прямой g при помощи горизонтально-конкурирующих точек 3 и 4. Фронтальная проекция точки 4 – 4₂, принадлежащая прямой g, располагается на фронтальной плоскости проекций выше проекции 3₂, следовательно, участок прямой g на горизонтальной плоскости проекций до точки пересечения К тоже будет видимым.

Дата добавления: 2014-01-07