Взаимное положение плоскостей

Плоскости могут быть параллельны между собой и пересекаться.

Две плоскости пересекаются по прямой линии, для определения которой достаточно найти две точки, принадлежащие этой линии. Так, прямая линия l, (рис. 50), по которой пересекаются между собой плоскость, заданная треугольником АВС, и плоскость g, одновременно принадлежит обеим плоскостям, значит, для определения данной линии необходимо на эпюре определить местонахождение двух любых точек этой прямой по их проекциям. Прямая линия, проходящая через эти точки, будет являться линией пересечения плоскостей.

Для решения подобных задач опять применяют вспомогательные проецирующие плоскости, но если хотя бы одна из плоскостей перпендикулярна к плоскости проекций, то построение линии пересечения упрощается. В данном параграфе рассматривается именно такой случай. Общий случай построения линии пересечения плоскостей, каждая из которых является плоскостью общего положения, в данном учебном пособии не рассматривается. Теоретический материал и примеры решения подобных задач можно найти в литературе, список которой приведен в конце пособия.

На рис. 51 показано пересечение двух плоскостей, из которых одна (заданная треугольником DEF) расположена перпендикулярно П₂. Так как треугольник DEF проецируется на плоскость П₂ в виде прямой линии, то фронтальная проекция отрезка прямой, по которой пересекаются оба треугольника, представляет собой отрезок 1₂3₂ на проекции D₂E₂F₂

При выполнении дальнейших построений определяется горизонтальная проекция отрезка прямой – 1 ₁ 3₁ и затем видимость сторон треугольников методом конкурирующих точек. Фактическим отрезком, по которому пересекаются треугольники, является отрезок 2 – 3. Определение проекций точки 2 ясно из чертежа.

Две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. Это утверждение служит основным признаком для определения, параллельны плоскости между собой или нет.

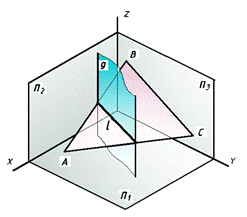
Рис. 50

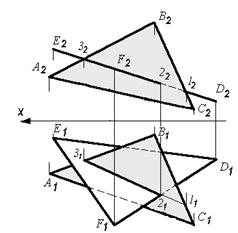
Рис. 51

Такими прямыми могут служить, например, следы обеих плоскостей: если два пересекающихся между собой следа одной плоскости параллельны одноименным с ними следам другой плоскости, то обе плоскости параллельны между собой (рис. 52).

На рис. 53 показаны параллельные между собой фронтально-проецирующие плоскости, заданные треугольниками. Их параллельность определяется параллельностью фронтальных проекций.

При построении плоскости через какую-либо точку пространства параллельно уже существующей, достаточно провести две пересекающиеся прямые через эту точку, которые будут параллельны двум любым пересекающимся прямым этой плоскости.

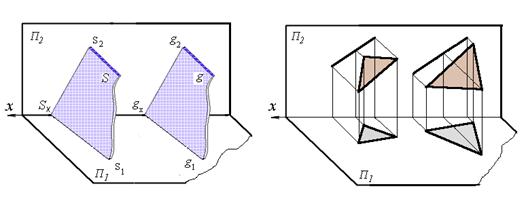
Рис. 52 Рис. 53

Дата добавления: 2014-01-07