Функции линейной электрической цепи

Под функциями линейных цепей понимают характеристики устойчивых линейных цепей, полностью и в наиболее удобной форме описывающие их электрические свойства.

На практике при анализе электрических цепей наиболее часто используют две функции линейных электрических цепей – комплексную функцию цепи и операторную функцию цепи.

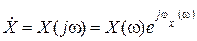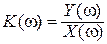Комплексная функция цепи – это комплексная функция частоты, равная отношению комплексной амплитуды отклика к комплексной амплитуде гармонического пробного сигнала , то есть . В последней записи – модуль комплексной функции цепи (в разделе 3 вводили понятие модуля комплексного коэффициента передачи), 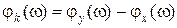– аргумент комплексной функции цепи (соответственно – аргумент комплексного коэффициента передачи). K (w) и j _k (w) называют соответственно амплитудно-частотной и фазочастотной характеристиками комплексной функции цепи и представляют соответствующими графиками.

В зависимости от размерностей пробного сигнала и отклика на него, а также от того, на одном или на разных полюсах цепи они действуют, комплексная функция цепи приобретает различный физический смысл, размерность и обозначение. Так, для четырехполюсника с входными и выходными 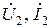переменными различают: коэффициент передачи по напряжению 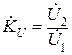, коэффициент передачи по току , передаточное сопротивление 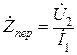и передаточную проводимость 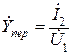. Для двухполюсника различают: входное сопротивление 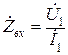и входную проводимость .

Когда воздействие и отклик имеют одинаковую размерность, функцию цепи (комплексную или операторную) называют передаточной функцией. Комплексная функция цепи описывает свойства линейной цепи в частотной области и лежит в основе спектрального метода анализа передачи сигналов.

Операторная функция цепи – это функция комплексной частоты (оператора Лапласа) р = s + j w, равная отношению лапласовых изображений отклика линейной цепи Y (p) = L { y (t)} и воздействия Х (р) = L { x (t)}, то есть .

Операторная функция цепи является обобщением комплексной функции цепи на случай комплексной частоты. Переход от комплексной функции цепи к операторной функции цепи достигается заменой j w на р. Операторная функция цепи, как и комплексная функция цепи, может иметь различный смысл: операторного коэффициента передачи по напряжению 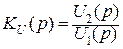, операторного коэффициента передачи по току , операторного передаточного сопротивления или операторной передаточной проводимости , операторных входного сопротивления 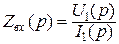или входной проводимости .

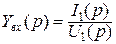Если линейная цепь не содержит независимых источников энергии, то ее операторная функция цепи является рациональной функцией р с действительными коэффициентами, то есть

,

где р ₀₁,..., р _{0 п} – решения уравнения F ₁(p) = 0, называемые нулями

операторной функции цепи;

р _п1,..., р _{п т} – решения уравнения F ₂(p) = 0, называемые полюсами

операторной функции цепи.

Дата добавления: 2014-01-07