Растяжение и сжатие

Растяжением или сжатием называется такой вид деформации, при кото­ром в поперечном сечении бруса возникает один ВСФ — продольная сила N. Она равна алгебраической сумме проекций на про­дольную ось внешних сил, действующих на отсеченную часть бруса:

Так как величина продольных сил в разных сечениях бруса неодинакова, то строится эпюра продольных сил. Эпюра продольных сил - график, показывающий изменения ве­личины продольных сил в сечении бруса по его длине.

Последовательность построения эпюр продольных сил:

1. Разбиваем брус на участки, ограниченные точками приложения сил (нумерацию участков ведем от незакрепленного конца).

2. Используя метод сечений, определяем величину продольных сил в се­чении каждого участка.

3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изобра­жением бруса (или рядом) проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответствующие в выбран­ном масштабе продольным силам (положительное значение откладываем вверх (или вправо), отрицательное — вниз (или влево)).

Под действием продольных сил в поперечном сечении бруса возникает нормальное напряжение, которое определяется по формуле: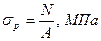

Где А — площадь поперечного сечения участка.

Гипотеза плоских сечений устанавливает, что при растяжении (сжатии) сечение бруса остается плоским и перпендикулярным линии действия силы. Закон Гука при растяжении - нормальное напряжение, возникающее в поперечных сечениях при растяжении в пределах упругости, прямо пропорционально продольной деформации:

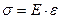
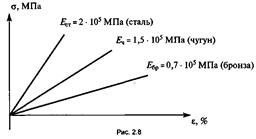
где Е — коэффициент пропорциональности, который называется модулем упругости.. Он характеризует жест­кость материала, из которого изготовлен элемент конструкции. Для различных материалов его значения определены экспериментально. Закон Гука можно изобразить графически (рис. 2.8).

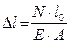Закон Гука для определения деформации растяжения:

где — абсолютное изменение продольных размеров; l₀ — первоначальные размеры элемента; ЕА — величина, характеризующая жесткость сечения бруса.

Условие прочности при растяжении: рабочее напряжение должно быть меньше или равно допускаемому напряжению, т.е.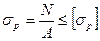

Используя это условие, можно выполнить три вида расчетов на прочность при растяжении.

1. Проверочный — проверка прочности: по заданной рабочей нагрузке и заданному размеру сечения определяем рабочее напряжение и сравниваем его с допускаемым напряжением. Если 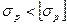- удовлетворяет условию проч­ности, если 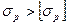- не удовлетворяет условию проч­ности

2. Проектный — подбор размера сечения по заданной рабочей нагрузке и допускаемому напряжению: (например для вала) -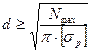

3. Проверочно-уточненный — определение допускаемого значения рабочей нагрузки по заданному размеру сечения и допускаемому напряжению. (например для круглого бруса):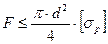

Дата добавления: 2014-01-07