Метод заключается в составлении системы уравнений по I и II ЗК, решение которой позволяет определить токи всех ветвей

Метод прямого применения законов Кирхгофа

ЛЕКЦИЯ 2

Классификация цепей и особенности их расчета

Электрические цепи классифицируются следующим образом:

- линейные, содержащие только линейные элементы, которые характеризуются неизменными значениями своих параметров вне зависимости от протекающих через них токов (приложенных к ним напряжений);

- нелинейные, в которых содержится хотя бы один нелинейный элемент;

- пассивные, которые не содержат источников питания;

- активные, содержащие источники питания;

- простые, содержащие один источник питания;

- сложные неразветвленные, содержащие один контур, но несколько источников питания;

- сложные разветвленные, в состав которых входят несколько контуров с источниками питания.

Принцип расчета цепей заключается в составлении уравнений математическими методами и решении этих уравнений относительно искомых электрических величин (токов, напряжений и т. п.). При записи уравнений необходимо показать условно положительные направления всех токов и напряжений схемы. Обычно заданы значения параметров всех источников энергии и элементов схемы. В ряде случаев исходную схему предварительно упрощают, используя эквивалентные преобразования.

Разветвленные цепи (сложные цепи) содержат несколько источников питания, расположенных в различных контурах. Для расчета сложных цепей применяют методы законов Кирхгофа, контурных токов, наложения, эквивалентного генератора, узлового напряжения (метод двух узлов).

Методика расчета следующая:

1) задаются произвольными направлениями токов в ветвях (токов столько, сколько ветвей);

2) задают направления обхода контуров (по направлению движения часовой стрелки или наоборот);

3) определяют число узловых точек n и число ветвей m;

4) составляют уравнения по I ЗК для n – 1 узловых точек;

5) недостающее число уравнений m – (n – 1) составляют по II ЗК для контуров.

Так, для электрической схемы, имеющей четыре узловых точек, шесть ветвей, составим уравнения по I и II ЗК, задав направление токов в ветвях и направление обхода контуров по часовой стрелке.

К пояснению расчета разветвленной цепи с помощью законов Кирхгофа

Составляем уравнения по I ЗК для трех узловых точек - 4, 6, 7.

4: I ₁ - I ₃ - I ₄ = 0;

6: I ₄ – I ₅ + I ₆ = 0;

7: I ₅ + I ₃ + I ₆ = 0.

Определяем число уравнений, составленных по II ЗК:

m – (n – 1) = 6 – (4 – 1) = 3.

Составляем уравнения по II ЗК для трех контуров:

m – (n – 1) = 6 – (4 – 1) = 3.

Составляем уравнения по II ЗК для трех контуров:

(1-4-7-1): E ₁ - Е ₂ = (R ₁ + R ₂) I ₁ + R ₃ I ₃ – R ₆ I ₆;

(7-4-6-7): Е ₂ + Е ₃ = - R ₃ I ₃ + R ₄ I ₄ + R ₅ I ₅;

(1–7–6-1): 0 = R ₆ I ₆ - R ₅ I ₅ - R ₇ I ₇.

Совместное решение шести уравнений дает возможность определить токи шести ветвей. Следует обратить внимание на знаки полученных токов. Если ток получен со знаком «-», это значит, что положительное направление тока обратно принятому произвольно. Тогда на электрической схеме надо показать действительные направления токов ветвей.

Метод наложения (суперпозиции)

Применение данного метода основано на принципе наложения (суперпозиции): в электрических цепях все источники работают независимо друг от друга и создаваемые совместно токи ветвей равны алгебраической сумме токов, создаваемых каждым из источников в отдельности.

Данный метод дает возможность свести расчет сложной цепи с несколькими источниками питания к нескольким расчетам этой же цепи с одним источником питания.

Расчет ведут в следующей последовательности:

1) поочередно рассчитывают токи ветвей от действия одной ЭДС, считая все остальные ЭДС равными нулю и оставляя их внутреннее сопротивление R ₀;

2) пункт 1 повторяется столько раз, сколько ЭДС в цепи;

3) определяют действительные токи ветвей, алгебраически суммируя токи, вызываемые в ветви каждой ЭДС в отдельности;

Так для электрической схемы с двумя источниками ЭДС Е _1, Е ₂ величины и направления токов I ₁, I ₂, I ₃, I ₄ определяются в следующей последовательности: оставляют источник питания Е ₁; Е ₂ = 0 (электрическая схема с одним источником ЭДС Е ₁).

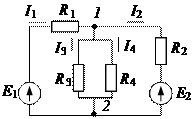
Электрическая схема с двумя источниками ЭДС (Е ₁, Е ₂)

Электрическая схема с источником ЭДС Е ₁

Так как сопротивления R ₂, R ₃, R ₄ включены параллельно, то

R _2,3,4 = R ₂ R ₃ R ₄/(R ₂ R ₃ + R ₃ R ₄ + R ₂ R ₄), R '_экв = R ₁ + R _2,3,4.

Ток I '_экв = E ₁ / R '_экв;

U '₁₂ = R _2,3,4 I; I '2 = U12 '/ R ₂;

I '₃ = U '₁₂/ R ₃; I '₄ = U '₁₂/ R4.

Далее определяют токи от Е ₂, полагая, что Е ₁ = 0 (электрическая схема с источником ЭДС Е₂)

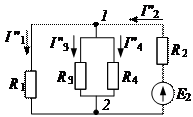
Электрическая схема с источником ЭДС Е ₂

R _1,3,4 = R ₁ R ₃ R ₄/(R ₁ R ₃ + R ₃ R ₄ + R ₁ R ₄);

R ''_экв = R ₂ + R _1,3,4;

I ''_экв = E ₂ R ''_экв

U ''₁₂ = R _1,3,4 I ₂''; I ''₁ = U ''₁₂/ R1;

I ''₃ = U ''₁₂/ R ₃; I ''₄ = U ''₁₂/ R ₄.

Действительные токи ветвей

I ₁ = I '₁ - I ''₁ ; I ₂ = I '₂ - I ''₂ ; I ₃ = I '₃ I ''₃; I ₄ = I '₄ I ''₄.

Направление токов І ₁ и І ₂ – направление большего по величине тока или .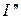

К пояснению метода наложения

На рисунке показаны направления тока І ₁ при условии , а І ₂ при условии .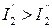

Дата добавления: 2014-01-07