Политропный процесс и его обобщающее значение

Политропным называется процесс, в котором возможно изменение всех термодинамических параметров состояния и может осуществляться теплообмен, но теплоёмкость в процессе остаётся постоянной.

Уравнение политропного процесса имеет вид

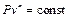, (5.28)

где n – показатель политропы, который может принимать любые положительные и отрицательные значения от – ∞ до + ∞.

Показатель политропы определяется по формуле

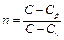, (5.29)

где C – теплоёмкость в данном политропном процессе, определяемая по формуле

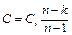. (5.30)

Теплоёмкость в политропном процессе также может принимать любые положительные и отрицательные значения от – ∞ до + ∞.

Обобщающее значение политропного процесса заключается в том, что все рассмотренные ранее процессы являются частными случаями политропного процесса в зависимости от показателя политропы n.

Например, подставив в уравнение политропного процесса (5.28) значение показателя политропы n = 0, получим уравнение изобарного процесса P = const. Подставив значение показателя политропы n = 0 в уравнение (5.30), получим величину теплоёмкости в процессе C = C_p, что также соответствует изобарному процессу. Аналогично можем получить уравнения и значения теплоёмкости для изотермического, адиабатного и изохорного процессов (табл. 4).

Сравнив уравнения адиабатного (5.17) и политропного (5.28) процессов, можно сделать вывод, что различие между ними только в показателе степени при множителе v. В адиабатном процессе показатель степени равен k, а в политропном – n, поэтому соотношения между начальными и конечными параметрами состояния в политропном процессе будут аналогичны соотношениям в адиабатном процессе с той лишь разницей, что вместо показателя адиабаты k в них используется показатель политропы n.

Таблица 4. Уравнение процесса и величина теплоёмкости в нём в зависимости от показателя политропы n

Показатель политропы в процессе	Уравнение процесса	Теплоёмкость в процессе
n = 0	Pv^n = const; P = const	C = Cv ∙ k = Cp
n = 1	Pv^n = const; Pv = const	C = ± ∞
n = k	Pv^n = const; Pv^k = const	C = 0
n = ± ∞	Pv^n = const; v = const	C = Cv

Тогда с учётом выражения (5.19) соотношение между давлением и удельным объёмом в политропном процессе примет вид

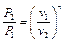. (5.31)

Из выражения (5.21) получим соотношение между абсолютной температурой и удельным объёмом:

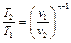, (5.32)

а из выражения (5.22) – между абсолютной температурой и давлением:

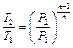. (5.33)

Работа расширения в политропном процессе может быть найдена по аналогии с адиабатным процессом (5.25) по формуле

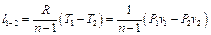, (5.34)

а полезная (располагаемая) работа – из выражения (5.27):

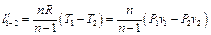. (5.35)

Изменение внутренней энергии Δ u и энтальпии Δ h в политропном процессе определяется по общим формулам (1.10) и (1.13):

,

.

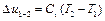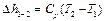Изменение энтропии Δ s в политропном процессе можно найти с помощью выражений (1.14) и (2.5):

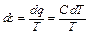, откуда ,

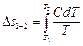и окончательно для политропного процесса получим выражение

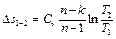. (5.36)

Количество теплоты, участвующей в политропном процессе, может быть определено по формуле

,

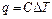откуда, используя выражение (5.30), получим

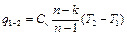. (5.37)

Дата добавления: 2014-01-07