Колебаний

Демодуляция амплитудно – модулированных

Демодуляция амплитудно – модулированных колебаний с двумя боковыми полосами (ДБП). Демодуляция, или выделение информационного сигнала называется детектированием.

Детектирование состоит из воздействия полученного амплитудно –модулированного сигнала (4-3) на нелинейный элемент.

Если воспользоваться уравнением вольт – амперной характеристики (4-9) и подставить в него выражение (4-3), то получим:

i = a ₀ + a ₁ U_ω0 (1 + m cosΩ t) cosω₀ t +

a ₂ U ² _ω0 (1 + m cosΩ t)² cos ² ω₀ t = a ₀ + 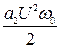(1 + ) + а ₂ U ² _ω0 m cosΩ t + a ₁+ 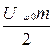cos (ω₀ – Ω) t + a ₁ U_ω0 cosω₀ t + а ₁ cos (ω₀ + Ω) t +

a ₂ cos 2 Ω t + a ₂ cos (2ω₀ – 2Ω) t + a ₂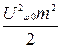 cos (2ω₀ – Ω) t + a ₂(1 + ) cos 2ω₀ t + a ₂ cos (2ω₀ + Ω) t a ₂ cos (2ω₀ + 2Ω) t. (4-11)

Из рис а), на котором представлен спектр сигнала, полученный на основании (4-11), следует, что кроме несущей F_ω0 и двух боковых частот (F_ω0 – F _Ω, F_ω0 + F _Ω), из которых состоял сигнал до детектирования, появился ряд частот как в частотной его части. Так, кроме частоты сообщения F _Ω, которую нам и необходимо выделить, есть еще постоянная составляющая [первые два члена в (4-11)] и вторая гармоника сообщения a ₂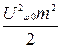 cos 2 Ω t. Следовательно, детектирование с использованием квадратичного нелинейного элемента, вольт – амперная характеристика которого представлена на рис. 4-3, б), всегда приводит к нелинейным искажениям.

Во избежание искажений при детектировании необходимо, чтобы нелинейный элемент обладал линейно – ломанной вольт – амперной характеристикой, представленной на рис. 4-3,в). Уравнение этой характеристики запишется:

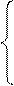
I

i = au при u > 0

u 0 при u < 0 (4-12)

Если воспользоваться элементом с уравнением характеристики

(рис. 4-3, г)

I

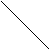
u i = a (u) (4-13)

и проделать расчеты, аналогичные выполненным выше, то получим спектр,

изображенный на рис. 4-8, б).

Из этого спектра легко выделяется без всяких искажений сообщение с частотой F _Ω. Вторая гармоника 2 F _Ω этой частоты при использовании линейно – ломаных вольт – амперных характеристик отсутствует. такое детектирование называется линейным.

Сам процесс детектирование состоит из выпрямление амплитудно – модулированных колебаний, в результате которого образуются импульсы несущей с огибающей, имеющей форуму колебания передаваемого сообщения, и выделения из этих импульсов исходного сигнала путем фильтрации ВЧ – составляющих спектра импульсов. Схема детектора с однополупериодным выпрямлением представлена на рис. 4-9, а).

В качестве детектора применяется диод, обратный ток которого практически близок к нулю. Выпрямление желательно осуществлять на линейно части вольт – амперной характеристике диода.

Простейшим фильтром нижних частот может служить конденсатор, подключенный параллельно сопротивлению нагрузки R _н. На вход детектра подается модулированное колебание Um (рис. 4-9, б). С выпрямителя на ФНЧ поступают колебания (рис. 4-9, в). На нагрузке R _н выделяется демодулированное сообщение.

Дата добавления: 2014-01-07