Кодирование факторов

Выбор интервалов варьирования факторами

При планировании цель экспериментатора состоит в том, чтобы для каждого уровня выбрать два (или несколько) уровня, на которых он будет варьироваться в эксперименте. В полном факторном эксперименте факторы варьируются на двух: нижнем и верхнем уровнях.

Представим координатную ось, на которой откладываются значения факторов, например, температуры изотермической выдержки бетона.

------------о---------------о--------------о----------- Т, С.

нижний уровень 80 верхний уровень

Если нулевой уровень имеет значение 80 С, тогда два других уровня указываются точками, симметричными относительно 80 С. В данном случае понятия "нижний" и "верхний" условны и могут быть не связаны с абсолютными значениями факторов, а для качественных факторов эти понятия вообще являются отвлеченными понятиями.

Интервалом варьирования называется некоторое числовое значение (для каждого уровня свое), прибавление которого к нулевому уровню дает значение верхнего уровня, вычитание из нулевого дает значение нижнего уровня.

Таким образом, задача выбора уровней сводится к простой задаче выбора интервалов варьирования факторами.

Для упрощения записей и формализации расчетов приняты следующие обозначения уровней факторов в так называемых кодированных значениях:

· нижний уровень – [–1] или просто [–],

· нулевой уровень – [0],

· верхний уровень – [+1] или [+].

Для количественных факторов с непрерывной областью определения преобразование натуральных значений факторов в кодированные значения следует осуществлять, используя выражение

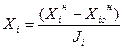(18)

J_i

где X_i –кодированное значение фактора; X_i^н –натуральное значение фактора; X_io^н –натуральное значение основного уровня фактора; J_i –натуральное значение интервала варьирования фактора; i –номер фактора

Для качественных факторов, имеющих два уровня, один обозначается [–1], другой [+1]. Порядок значения не имеет.

Задача № 13. Пусть в задаче оптимизации процесса тепловой обработки бетона факторами выбраны: X₁ – температура изотермической выдержки, С, X₂ – длительность периода изотермической выдержки, час. Основной уровень и интервалы варьирования приведены в табл. 3

Таблица 3

Уровни	X1^н	X2^н
Основной уровень
Интервал варьирования

Условия одного из опытов в кодированных выражениях выглядят следующим образом: X₁ = –0,5, X₂ =0,5. Определить правильные натуральные значения факторов данного опыта.

На выбор интервалов варьирования факторами накладываются ограничения снизу и сверху. Интервал варьирования не может быть меньше той ошибки, с которой фиксируется уровень фактора. В противном случае нижний и верхний уровни будут статистически неразличимы.

2.11. Составление план – матрицы эксперимента

После выбора основного уровня и интервалов варьирования строится план эксперимента. Первый этап планирования эксперимента для построения линейной модели основан на варьировании факторов на двух уровнях. При этом число опытов (состояний объекта) определяется из уже известной формулы N=2^k, где k – число факторов. Эксперимент, в котором реализуются все возможные сочетания уровней факторов называется ПОЛНЫМ ФАКТОРНЫМ ЭКСПЕРИМЕНТОМ. Условия эксперимента удобно записывать в виде таблицы (матрицы), где строки (называемые вектор – строками) соответствуют различным опытам, а столбцы (вектор – столбцы) – соответствуют значениям факторов (табл. 4).

Таблица 4

№	X1	X2	Y	Буквенное обозначение
	-1	-1	Y1
	+1	-1	Y2	a
	-1	+1	Y3	b
	+1	+1	Y4	ab

Графически точки матрицы планирования изображены на рис.5.

Площадь, ограниченная квадратом называется, областью эксперимента.

В задачах интерполяции область эксперимента есть область предсказываемых значений параметра оптимизации.

Существует иная форма записи матрицы планирования: порядковый номер фактора ставится в соответствии строчной букве латинского алфавита: X₁ – a, X₂ – b, X₃ – c и т.д. Если для строки матрицы выписать буквы только для тех факторов, которые находятся на верхних уровнях, то условия опытов при этом задаются однозначно. Опыт со всеми факторами на нижних уровнях обозначается как [+1] (табл.5).

Для двух факторов все возможные комбинации факторов легко находятся простым перебором. С ростом числа факторов построение матрицы усложняется.

Существуют простые приемы построения матриц ПФЭ.

1. При добавлении нового фактора каждая комбинация уровней исходного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Поэтому следует записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня.

Таблица 5

№	X1	X2	X3
	–1	–1	–1
	+1	–1	–1
	–1	+1	–1
	+1	+1	–1
	–1	–1	+1
	+1	–1	+1
	–1	+1	+1
	+1	+1	+1

2. Второй прием основан на чередовании знаков. В первом столбце знаки меняются поочередно, во втором – через два, в третьем – через четыре, в четвертом – через восемь и т.п.

В общем случае для линейных моделей ПФЭ типа 2² геометрический образ модели представляет гиперплоскость в (K+1)-мерном факторном пространстве, что исключает возможность зрительного восприятия образа, кроме случая, когда К=2 (рис. 4).

По аналогии с ПФЭ 2² можно дать графическую интерпретацию ПФЭ 2³. Это куб с точками опытов в его вершинах. Фигура, которая задает область эксперимента в многомерном пространстве при числе факторов K > 3 носит название гиперкуба.

Рассмотрим некоторые свойства матриц, определяющие качество моделей.

Эксперимент планируется для того, чтобы получить математическую модель, обладающую некоторыми оптимальными свойствами: оценки коэффициентов модели должны быть наилучшими; точность предсказаний параметра оптимизации не должна зависеть от направления в факторном пространстве. Итак, что же это за свойства?

Сначала рассмотрим свойства отдельных столбцов матрицы.

1. Симметричность относительно центра эксперимента: алгебраическая сумма элементов вектора-столбца каждого фактора равна нулю

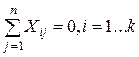. (19)

2. Условие нормировки: сумма квадратов элементов каждого столбца равна числу опытов

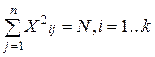. (20)

Теперь рассмотрим свойства совокупности столбцов.

3. Ортогональность матрицы планирования: сумма почленных произведений любых двух вектор – столбцов матрицы равна нулю.

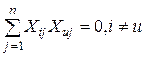. (21)

4. Ротатабельность матрицы: точки в матрице планирования подбираются таким образом, чтобы точность предсказаний значений параметра оптимизации была бы одинакова на равных расстояниях от центра эксперимента в независимости от направления рассмотрения.

Дата добавления: 2014-01-07