Расчет коэффициентов полного факторного эксперимента. Эффекты взаимодействия. Смешанные оценки

Реализация эксперимента

Рандомизация опытов

На изучаемый процесс кроме варьируемых факторов оказывают влияние и другие, зачастую неизвестные исследователю. Для того, чтобы внести элемент случайности влияния этих факторов на результаты опыта, устанавливается случайный порядок постановки опытов во времени. Эта процедура и называется рандомизацией. Для ее осуществление можно использовать таблицы случайных чисел, лотерею и т.п.

Реализация плана предполагает проведение опытов в соответствии с условиями план – матрицы при обеспечении заданных систем ограничений эксперимента во времени и пространств.

Разберем дальнейшие расчеты на конкретном примере.

Упражнение № 5 Построить на данных табл. 6 математическую модель процесса влияния добавок CaCl₂ (X₁) и С – 3 (X₂) на прочность равноподвижных бетонных смесей через 28 суток нормального твердения.

Таблица 6

№	X0	X1	X2	X1X2	Единичные значения прочности, МПа	Среднее значение прочнос-ти, МПа	S^2yi, МПа	Расчетные значения прочности, МПа
	+1	–1	–1	+1	10, 8,9			7,25
	+1	+1	–1	–1	33, 27, 30			31,75
	+1	–1	+1	–1	14, 18, 16			17,75
	+1	+1	+1	+1	40, 48, 44			42,25

2.14. Проверка воспроизводимости опытов план – матрицы

При одинаковом числе параллельных результатов опыта на каждом сочетании уровней факторов воспроизводимость процесса проверяется по расчетному значению критерия Кохрена, при несовпадении – по критерию Фишера.

Процесс считается воспроизводимым, если соответствующие расчетные значения критериев не превышают табличных значений. Если это не выполняется, необходимо принять меры к уточнению измерений в опыте с максимальной дисперсией.

В рассматриваемом нами примере построчные дисперсии приведены в табл. 6.

Критерий Кохрена G_расч =16/30=0,533. Табличное значение критерия Кохрена (прил. Г) G _(0.05,2,4)=0,7679. Так как выполняется неравенство G_расч <G, следовательно воспроизводимость опытов в строках матрицы удовлетворительная.

Для план – матрицы лучшей оценкой дисперсии будет средняя арифметическая дисперсий по строкам плана, называемая дисперсия воспроизводимости S²_{y} (ошибкой опыта).

Величина дисперсии воспроизводимости в рассматриваемом примере S²_{y} =30/4=7,5.

В случае воспроизводимого процесса рассчитываются коэффициенты регрессии.

Целью реализации план - матриц как в задачах оптимизации, так и в задачах интерполяции – получение математических моделей, то есть определение неизвестных коэффициентов полинома. Для линейной модели полином выглядит как Y= b₀+b₁X₁ + b₂X₂. Рассматривая математические модели как объект исследования, следует помнить, что как и для других физических величин, для моделей существуют понятия истинного значения коэффициентов и экспериментальной оценки этого значения. Планируя и реализуя эксперимент, мы пытаемся провести проверку адекватности математической модели.

Эксперимент, имеющий конечное число опытов, позволяет получить выборочные оценки коэффициентов уравнения: b₀, b₁, b₂ и т.д. Их точность и надежность зависят от свойств выборки и определяются известными статистическими методами.

Для расчета коэффициентов полного факторного эксперимента следует пользоваться формулой

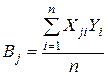; j=1…k. (22)

n

Подсчет оценок коэффициентов ПФЭ типа 2² по формуле (22) дает следующие результаты

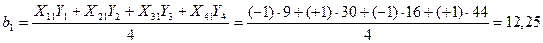
Аналогичным образом расчет b₂ дает значение 5,25.

Благодаря кодированию факторов расчет коэффициентов полностью формализован. Если уравнение Y=b₀+b₁X₁+b₂X₂ справедливо, то оно справедливо и для средних значений переменных факторов =b₀+b₁++b₂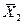, а так как в силу симметрии = =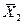0, то b₀= , то есть мы определяем значение свободного члена полинома. Чтобы привести оценку свободного члена в соответствие с общей формулой расчета (22) коэффициентов модели поступают следующим образом: в матрицу планирования помещают дополнительный вектор-столбец фиктивной переменной X₀, которая для всех опытов принимает значение [+1]. Тогда b₀ =24,5.

Свободный член уравнения является оценкой параметра оптимизации в центральной точке плана. Но такой же столбец X₀ надо было бы использовать и при расчете оценки квадратичных эффектов X²₁, X²₂. Следовательно, по результатам реализации ПФЭ оценка свободного члена является смешанной с суммарной оценкой квадратичных эффектов всех факторов. Если квадратичные эффекты будут значимы, прогнозируемый результат опыта в центральной точке эксперимента будет существенно отличаться от экспериментального значения, и следует переходить к планам второго порядка.

Окончательно полином первой степени вида в рассматриваемой задаче имеет вид Y= 24,75 + 12,25 X₁+ 5,25 X₂.

Коэффициенты при независимых переменных указывают на силу влияния факторов: чем больше численная величина коэффициента, тем большее влияние оказывает фактор на параметр оптимизации. Если знак коэффициента [+], то с увеличением значения фактора параметр оптимизации увеличивается, и наоборот. Величина коэффициента соответствует вкладу данного фактора в значение параметра оптимизации при переходе фактора с нулевого уровня на верхний или нижний. Но чаще, а особенно для качественных факторов, вклад фактора в параметр оптимизации оценивают по ЗНАЧЕНИЮ ЭФФЕКТА ФАКТОРА, представляющему собой значение вклада фактора в параметр оптимизации при переходе с нижнего на верхний уровень. Численно эффект фактора равен удвоенному значению коэффициента с сохранением знака.

Если линейная модель адекватна, то поставленная задача решена. В экстремальных задачах далее продолжается восхождение по градиенту, в интерполяционных – эксперимент заканчивается. А если линейная модель неадекватна? Можно ли, используя результаты ПФЭ, оценить нелинейность модели? Да. Один из часто встречающихся видов нелинейности связан с тем, что эффект фактора зависит от уровня, на котором находится другой фактор. В этом случае говорят, что имеется эффект взаимодействия факторов. Для его количественной оценки в матрицу планирования дополнительно помещается вектор столбец произведений двух факторов X₁X₂. При вычислении значения коэффициента взаимодействия пользуются известной уже формулой (22), поступая со столбцом взаимодействия так же, как с обычным столбцом матрицы. Заметим, что добавление в матрицу вектор – столбца эффекта взаимодействия фактора не изменяет свойств матрицы. Следует обратить внимание на то, что в задачах оптимизации необходимо стремиться сделать эффекты взаимодействия как можно меньшими, а в задачах интерполяции наоборот, выявление эффектов взаимодействия представляет собой практический интерес.

Дата добавления: 2014-01-07