
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №3. Тема: Динамика вращательного движения
|
|
|
|
Тема: Динамика вращательного движения. Момент силы относительно точки и оси. Момент инерции твердого тела относительно оси вращения. Теорема Штейнера. Основной закон динамики вращательного движения. Момент импульса твердого тела относительно оси вращения. Закон сохранения момента импульса.
При вращательном движении все частицы твердого тела описывают окружности вокруг оси вращения тела. Угловая скорость  и ускорение ε для частиц тела одинаковы. Линейные скорость V и ускорение
и ускорение ε для частиц тела одинаковы. Линейные скорость V и ускорение 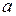 пропорциональны расстоянию
пропорциональны расстоянию 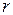 частицы от оси вращения (
частицы от оси вращения ( ). Если тело может вращаться только вокруг неподвижной оси, то способность силы F вращать тело вокруг этой оси характеризует момент силы относительно оси M.
). Если тело может вращаться только вокруг неподвижной оси, то способность силы F вращать тело вокруг этой оси характеризует момент силы относительно оси M.
Момент силы относительно оси представляет собой осевой вектор, направленный по оси вращения, и определяется по правилу правого буравчика. В общем случае записывается:
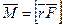 ,
,
где 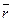 – радиус-вектор;
– радиус-вектор; 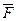 – сила.
– сила.
Вращающееся тело, как всякое движущееся тело, обладает кинетической энергией:
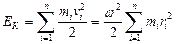 .
.
Сумма произведений масс элементарных частей тела на квадраты их расстояний до определенной оси называется моментом инерции тела относительно этой оси:
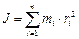 .
.
Для сплошного тела момент инерции выражается интегралом:
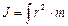 .
.
С учетом этого кинетическая энергия вращающегося тела:
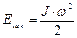 .
.
Величина момента инерции существует безотносительно к вращению.
Момент инерции тонкого стержня длиною l относительно оси симметрии: J = 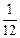 ml2, относительно оси, проходящей через конец стержня: J =
ml2, относительно оси, проходящей через конец стержня: J = 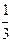 ml 2.
ml 2.
Момент инерции бруска длиною a и шириною b относительно оси симметрии: J =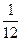 m(a2+b2).
m(a2+b2).
Момент инерции тонкостенного кольца (обруча) радиусом R относительно оси симметрии: J = m . R2.
Момент инерции диска (сплошного цилиндра) радиусом R, вращающегося вокруг оси, проходящей через центр диска перпендикулярно плоскости диска J =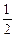 mR2.
mR2.
Момент инерции шара радиусом R относительно оси симметрии: J = 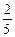 mR2.
mR2.
Если ось вращения тела параллельна оси симметрии, но смещена от нее на расстояние l, то момент инерции J 1 относительно параллельно смещенной оси выражается соотношением
J1 = J + ml2
где J – момент инерции относительно оси симметрии, имеющей название теоремы Штейнера. Зависимость между моментом инерции тела и моментом силы, вызвавшим вращение тела, называется основным уравнением динамики вращательного движения и записывается: .
.
Это выражение можно записать и так:
М = Jε = J =
= 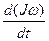 .
.
В последнем выражении 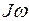 – есть момент количества движения относительно оси вращения. Для замкнутой системы момент внешних сил М равен нулю, тогда
– есть момент количества движения относительно оси вращения. Для замкнутой системы момент внешних сил М равен нулю, тогда
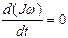 или J
или J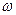 = const.
= const.
В заключение покажем аналогию между величинами, характеризующими
поступательное движение, и соответствующими величинами вращательного движения (табл.).
| Движения | |
| Поступательные |  Вщательные Вщательные
|
| Линейное перемещение S Линейная скорость V | Угловое перемещение 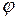 Угловая скорость Угловая скорость 
|
Линейное ускорение 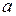 Сила F Сила F
| Угловое ускорение ε Момент силы M |
| Количество движения mV Импульс силы Ft | Момент количества движения 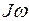 Момент импульса силы Mt Момент импульса силы Mt
|
| Масса m | Момент инерции 
|
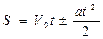
| 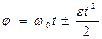
|
V = V0 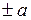 t t
| 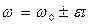
|
F = mа = 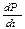 A = Fds
A = Fds
| M = Jε = 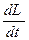 A = Md
A = Md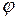
|
N = FV
E К = 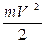
| N = M EК =
EК = 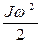
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 250; Нарушение авторских прав?; Мы поможем в написании вашей работы!