Лекция №4. Тема: Элементы механики жидкостей

Тема: Элементы механики жидкостей. Давление в жидкости и газе. Уравнение неразрывности. Уравнение Бернулли и следствие из него. Вязкость (внутреннее трение). Ламинарный и турбулентный режим течения жидкостей. Методы определения вязкости.

Жидкость считается идеальной, если перемещение одних частей жидкости относительно других не вызывает сил трения, т. е. внут­реннее трение (вязкость) отсутствует.

Уравнение Бернулли для стационарно текущей трубки идеальной жидкости записывается:

,

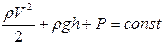где 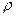– плотность несжимаемой жидкости; 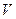– скорость в сечении выбранной трубки жидкости; 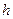– высота трубки жидкости; P – гидравлическое давление (статическое давление).

Статическое давление – давление внутри жидкости, т. е. давление жидкости на поверхность обтекаемого ею тела.

Уравнение достаточно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.

Если молекулы отличаются одна от другой какой-либо характер­ной величиной (энергией, массой, импульсом и др.), причем их распределение по значениям указанной характеристики неоднородно, то вследствие теплового движения молекул эта величина переносится из одного места в другое. В результате возникает поток рассматри­ваемой величины, обуславливающий ряд явлений, называемых явлениями переноса. К ним относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение или вязкость (обусловлено переносом импульса). Реальная жидкость в отличие от идеальной обладает вязкостью, обусловлен­ной сцеплением между ее молекулами. Единицей вязкости в системе СИ является Паскаль-секунда и обозначается – Па·с. Вязкость жид­кости во много раз превосходит вязкость газов. Вязкость жидкости находится в пределах (10^-3 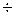1) Па·с и с повышением температуры уменьшается. Например, у воды при 0°С 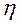=1,8 10^-3 Па ^. с, а при 90°С 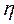= 3,2 10^-4 Па·с. Необходимо различать в движении жидкос­ти два вида ее течения:ламинарное (параллельными слоями) и тур­булентное (перемешивающееся, вихревое). Английский ученый Рейнольдс установил, что характер течения зависит от значения безраз­мерной величины:

R_e = ,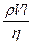

где 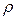– плотность жидкости (газа); V – средняя скорость потока; 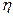– коэффициент вязкости; l – ха­рактерный для поперечного сечения потока размер. Величина Rе называется числом Рейнольдса. При малых значениях R_e 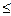1000 наблюдается ламинарное течение. При значении R_e 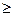1000 течение приобретает турбулентный характер. Число Рейнольдса может служить критерием подобия для течения жидкости в трубах, каналах и т. д. Характер течения различных жидкостей (газов) в трубах разных сечений будет совершен­но одинаков, если каждому течению соответствует одно и то же значение R_e.

Благодаря вязкости тело, движущееся в жидкости, увлекает прилегающие к нему слои жидкости и потому испытывает сопро­тивление (трение) со стороны жидкости. Сила сопротивления за­висит от скорости движения тела, его размеров и формы. Стокс установил, что при малых R_e или небольших скоростях движения тел шарообразной формы сила сопротивления жидкости пропорцио­нальна вязкости жидкости 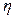, радиусу шара r и скорости дви­жения V, таким образом:

F = 6.

Закон Стокса применим также к движению шарообразных тел в газе, например к случаю падения дождевых капель в атмосфере.

Раздел 2.Молекулярная физика и термодинамика.

Дата добавления: 2014-01-07