
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №15. Тема : Колебания. Понятие колебательного движения
|
|
|
|
Тема: Колебания. Понятие колебательного движения. Гармонические колебания. Кинематика и динамика механических колебаний. Математический и физический маятники. Энергия гармонических колебаний.
Колебаниями называются любые движения, точно или приближенно повторяющиеся, через одинаковые промежутки времени.
Периодическими называются такие колебания, в которых каждое значение изменяющейся величины повторяется неограниченное число раз через одинаковые промежутки времени. Наименьшее время, за которое повторяется каждое значение изменяющейся величины, называется периодом колебания и обозначается буквой T. Величина, обратная периоду колебания 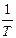 , называется частотой периодических колебаний и
, называется частотой периодических колебаний и  обозначается буквой ν. Единицей измерения частоты колебаний в системе СИ является герц – частота, при которой совершается одно колебание в секунду.
обозначается буквой ν. Единицей измерения частоты колебаний в системе СИ является герц – частота, при которой совершается одно колебание в секунду.
Простейшими являются гармонические колебания, то есть такие, при которых периодическое изменение величины (смещения) выражается косинусоидальным (или синусоидальным) законом: 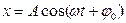 ,
,
где А – амплитуда колебаний – величина, равная наибольшему (по модулю) значению изменяющейся величины;(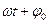 ) – фаза гармонического колебания;
) – фаза гармонического колебания; 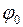 – начальная фаза;
– начальная фаза;  – угловая частота:
– угловая частота:
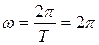 ν.
ν.
Фаза гармонического колебания определяет значение изменяющейся величины (наряду с амплитудой) в данный момент времени. Фаза измеряется в угловых единицах (радианах или градусах).
Для гармонических колебаний 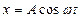 сила может быть математически записана так:
сила может быть математически записана так:
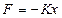 , где K =
, где K =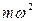
Частота гармонических колебаний: ν = 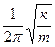 .
.
Период колебаний: 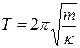 .
.
Полная энергия колеблющегося тела определяется суммой кинетической и потенциальной энергий:
Е = Eк+Eп=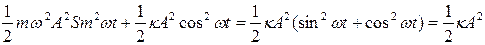 .
.
Полная энергия гармонического колебания пропорциональна квадрату амплитуды и коэффициенту упругости. В процессе движения происходят непрерывный переход кинетической энергии в потенциальную и обратно, но сумма их остается при этом постоянной.
Рассмотрим примеры гармонического колебательного движения под действием квазиупругих сил.
Маятник называется точечным (или математическим), если можно считать, что его масса сосредоточена в одной точке. Колебания математического маятника при малых углах отклонения можно считать гармоническими.

 0
0
 φ l
φ l


 Pt
Pt
 |
P Pn
Математический маятник
Период колебания математического маятника:
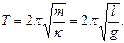
Материальное тело, подвешенное в точке, не совпадающей с центром тяжести тела, называется физическим маятником. Как и в случае математического маятника, угол 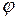 не более 5-6°. Для вращающегося тела рольмассыбудет играть момент инерции
не более 5-6°. Для вращающегося тела рольмассыбудет играть момент инерции  , а в качестве силы – момент силы
, а в качестве силы – момент силы 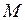 .
.

 L
L
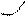


 0 e1
0 e1


 φ ц
φ ц

 Pt е2 01
Pt е2 01
P
Физический маятник
Период физического маятника:
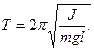
Если сравнить эту формулу с формулой для математического маятника, то 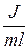 соответствует длине, которую обозначили
соответствует длине, которую обозначили 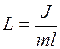 и назвали приведенной длиной физическогомаятника. Тогда и для физического маятника период ко-лебания будет вычисляться по формуле:
и назвали приведенной длиной физическогомаятника. Тогда и для физического маятника период ко-лебания будет вычисляться по формуле:
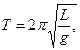
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 478; Нарушение авторских прав?; Мы поможем в написании вашей работы!