Свободные, затухающие и вынужденные колебания

Во всякой реальной колебательной системе обычно имеют место силы трения (сопротивления), действие которых приводит к уменьшению энергии системы. Сила трения выражается формулой:

где r – коэффициент трения, а знак минус указывает, что на­правление силы всегда противоположно скорости движения.

Если силы трения отсутствуют, формула (2.4) дает диффе­ренциальное уравнение:

которое имеет, решение в виде:

где ω₀ = . Колебания, происходящие при отсутствии сил трения, называются собственными или свободными. Частота собственных колебаний зависит только от свойств системы.

Допустим теперь, что в системе действуют две силы: F_УПР и F_ТР. Уравнение движения тела будет иметь вид:

Разделим это уравнение на массу тела и обозначим: .

Тогда получим дифференциальное уравнение затухающих колебаний, энергия которых уменьшается с течением времени:

Этому уравнению удовлетворяет функция: х = А₀ е^-dt Cos (wt + j₀),

где Значит, сейчас уже частота колебания зависит от , 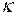и . Амплитуда колебания будет с течением време­ни изменяться по экспоненциальному закону . Величина , определяющая быстроту убывания амплитуды колебания с течением времени, называется коэффициентом затухания. Произ­ведение коэффициента затухания на период колебания T, равное логарифму отношения двух соседних амплитуд:

; ; -,

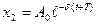есть безразмерная величина, и называется логарифмическим декре­ментом затухания. Колебания, происходящие в системе при нали­чии сил трения, называются затухающими. Частота этих колебаний зависит от свойств системы и интенсивности потерь (с их увеличением частота уменьшается). Для получения незату­хающих колебаний система должна подвергаться действию еще и внешней силы, непрерывно изменяющейся со временем по какому-нибудь закону. В частности, предположим, что внешняя сила явля­ется синусоидальной:

тогда уравнение движения тела будет иметь вид:

Разделим это уравнение на массу тела и к ранее принятым обозна­чениям добавим . В этом случае уравнение примет вид:

Уравнение характеризует уже вынужденные незатухающие ко­лебания под действием внешней периодической силы. Решение этого уравнения имеет вид:

x = A Cos (ωt-φ),

где А – амплитуда колебания, φ – фаза, равная: φ = аrctg .

Амплитуда вы­нужденных колебаний системы:

где – угловая частота собственных колебаний системы; – угловая частота вынуждающей силы.

При вынужденных колебаниях имеет место явление резонан­са, вызывающее резкое увеличение амплитуды вынужденных колеба­ний при совпадении собственной угловой частоты колебаний и уг­ловой частоты вынуждающей силы. Поскольку вынужденные колеба­ния имеют широкое применение в технике, то явление резонанса должно всегда учитываться, ибо оно может быть полезным в от­дельных процессах, а может быть и опасным явлением.

Важное место в машиностроении занимают вибрации (от лат. vibratio – колебание) – меха­нические колебания упругих тел различной формы. Это понятие обычно применяется по отношению к механическим колебаниям дета­лей машин, конструкций и сооружений, рассматриваемых в инженер­ном деле.

Раздел 5. Физика волновых процессов

Дата добавления: 2014-01-07