Сложение гармонических колебаний. Тема : (продолжение) Сложение колебаний

Лекция №16

Тема: (продолжение) Сложение колебаний. Собственные, затухающие и вынужденные колебания. Автоколебательные системы. Резонанс.

Колебания тела могут происходить под действием нескольких сил, действующих в разных направлениях, поэтому рассмотрим некоторые простые случаи сложения гармонических колебаний.

1. Сложение двух колебаний одного направления.

а) частоты и фазы – одинаковые, амплитуды разные:

X ₁ = a ₁ sin w t и X ₂ = a ₂ sin w t

Результат будет следующим: X = X ₁ + X ₂ = (a ₁ + a ₂) sin w t = A sinw t, т. е. амплитуда результирующего колебания будет равна сумме амплитуд складываемых колебаний;

б) частоты и амплитуды одинаковы, фазы отличаются на j:

X ₁ = a sin w t и X ₂ = a sin(w t + j).

Складывая, получим: X = X ₁ + X ₂ = 2 a cos j/2 sin(w t +j/2) = A sin (w t +j/2).

Амплитуда результирующего колебания A = 2 a cos j/2 меньше суммы амплитуд складываемых колебаний; в частности если j = p, то A = 0, т. е. два колебания с противоположными фазами взаимно друг друга гасят, и тело будет покоиться;

в) амплитуды одинаковы, j_о = 0, частоты различные:

X ₁ = a sin w₁ t и X ₂ = a sinw₂ t.

Складывая, получим: X = X ₁ + X ₂ = 2 a cos 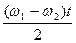sin 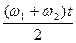^. = 2 a cos w_o t sin w t,

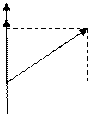
2. Сложение колебаний, происходящих в двух перпендикулярных направлениях. Обозначим смещение тела в одном направлении через X, а в другом – через Y: а) частоты и фазы – одинаковые, амплитуды различаются: X = a ₁ sin w t и Y = a ₂ sin w t. Совместное решение приводит к уравнению Y = a ₂ X/a ₁, т. е. результирующее колебание происходит вдоль прямой, составляющей с осью OX некоторый угол j, тангенс которого равен отношению a ₂ /a ₁, и графически может быть представлено так:

у

φ x

r = r₀Sinωt 0 x = a₁Sinωt

Расстояние r от колеблющегося тела до точки 0 будет изменяться со временем по формуле:

r =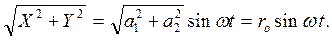

Результирующее колебание происходит вдоль прямой, составляющей с осью ОХ некоторый угол j, тангенс которого равен отношению ;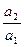

б) частоты одинаковы, фазы отличаются на p/2, амплитуды могут быть различны: X = a ₁ sin w t и Y = a ₂ sin (w t+ p/2)= a ₂cos w t. Результи рующее колебание характеризуется уравнением 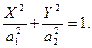Из аналитической геометрии известно, что данное выражение является уравнением эллипса. Следовательно, при сложении двух взаимно перпендикулярных колебательных движений, когда фазы колебаний отличаются на p/2, возникает движение по эллипсу, полуоси которого равны соответственно амплитудам складываемых колебаний. Если сложить колебательные движения с равными амплитудами (а ₁ = а ₂), то полученное уравнение траектории будет окружностью с радиусом, равным амплитуде, т. е. X²+ Y²=a²;

в) частоты разные, но кратные между собой, например w₁: w₂ = 1: 2; 2: 3 и т. д. В этом случае колеблющееся тело совершает движение по довольно сложным замкнутым траекториям, которые называют фигурами Лиссажу.

Форма этих фигур определяется отношением частот складывающихся колебаний, их амплитудами и разностью фаз между ними. Разобраться в сложностях этих колебаний помогает теорема Фурье, позволяющая представлять их совокупностью гармонических колебаний.

Оказывая воздействие на колеблющееся тело, можно вызвать изменение со временем амплитуды А=A(t) или частоты w = w (t) колебаний по какому-либо закону (в частности, периодическому):

X = A(t) sin (w t+j); X = A sin [w (t)t+j ]. Такие колебания называются модулированными. Модуляция называется амплитудной, если изменяется амплитуда при постоянной частоте колебаний, и частотной, если изменяется частота колебаний при постоянной амплитуде. Модуляция колебаний необходима, например, при радиопередачах; колебания, вызванные в микрофоне голосом диктора или звучанием музыкальных инструментов, изменяют амплитуду или частоту колебаний тока в антенне радиопередатчика. В приёмниках производится демодуляция колебаний (т. е. выделение тех воздействий, которые производили модуляцию), усиление их и обратное превращение в звуковые колебания.

Дата добавления: 2014-01-07