Дві прямі

Дві прямі можуть перетинатися, бути паралельними або мимобіжними. Якщо дві прямі перетинаються між собою, то точки перетину їхніх

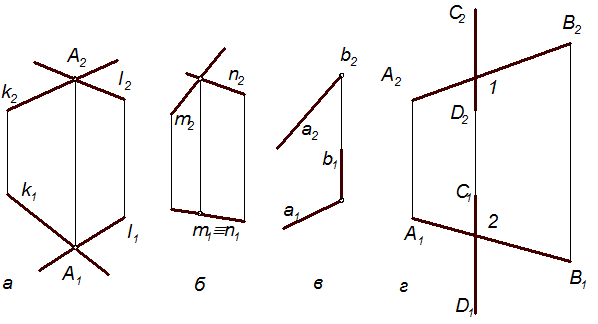однойменних проекцій належать одній лінії зв’язку (рис. 2.17). Проекції прямих, що перетинаються, можуть перетинатися (рис. 17, а), збігатися

Рис. 2.17

(рис. 17, б) або одна із проекцій прямих вироджується у точку, яка належить проекції іншої прямої. Твердження, що прямі перетинаються, якщо точки перетину їхніх однойменних проекцій належать одній лінії зв’язку, справедливе лише для прямих загального положення. На рис. 2.17, г точки перетину однойменних проекцій прямих AB(A₁B₁, A₂B₂) і CD(C₁D₁, C₂D₂) належать одній лінії зв’язку хоча подані прямі не перетинаються, бо C₂1/1D₂ 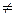C₁2/2D₁ (властивості аралельних проекцій).

Проекції паралельних прямих можуть бути паралельними рис. 2.18, а), збігатися (рис. 18, б) або вироджуватися у дві окремі точки (рис. 18, в).

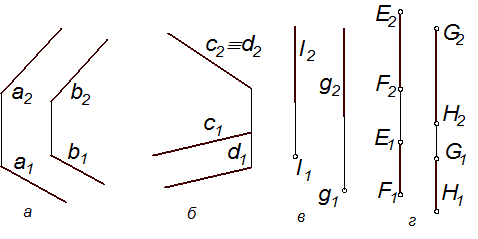Твердження, що прямі паралельні, якщо їхні однойменні проекції паралельні, справедливе за наявності проекцій прямих на трьох площинах проекцій або не менше, як на двох проекціях для прямих загального положення. Наприклад, якщо задані фронтальна і горизонтальна проекції двох профільних прямих, то ці прямі можуть бути або паралельними, або мимобіжними. На рис. 2.18, г подані дві профільні прямі EF(E₁F₁, E₂F₂) та GH(G₁H₁, G₂H₂). Хоча їхні фронтальні і горизонтальні проекції паралельні між собою, все ж самі прямі не Рис. 2.18

паралельні. У

цьому можна переконатися, побудувавши профільну проекцію. Правда, про непаралельність прямих EF і GH можна взнати і із фронтальної та горизонтальної проекцій, якщо порівняти довжини проекцій відрізків цих прямих. На рис. 2.18, г видно, що E₂F₂/G₂H₂ 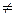E₁F₁/G₁H₁, а це означає, що прямі не паралельні.

Мимобіжні прямі - це прямі, які не перетинаються і не паралельні між собою. Точки перетину однойменних проекцій мимобіжних прямих не належать одній лінії зв’язку. На рис. 2.19, а показані дві мимобіжні прямі KL(K₁L₁, K₂L₂) і GH(G₁H₁, G₂H₂). У точках перетину горизонтальних проекцій цих прямих знаходяться проекції двох точок, одна з яких належить одній прямій, а друга - іншій. Ці дві точки розташовані на одному проекціювальному промені і називаються конкуруючими.

Вони використовуються для визначення видимості геометричних елементів на кресленнях. Наприклад, у перетині проекцій K₂L₂ і G₂H₂ знаходяться проекції 1₂ і 2₂ точок 1 і 2, із яких точка 1 належить Рис. 2.19

прямій KL, а точка 2 – прямій GH. З горизонтальної проекції видно, що точка 2 знаходиться перед точкою 1, тобто точка 2 закриває точку 1, тому точка 1 на фронтальній проекції вважається невидимою. Це означає, що пряма GH проходить перед прямою KL, тобто пряма GH закриває собою точку 1 прямої KL.

У перетині горизонтальних проекцій K₁L₁ та G₁H₁ прямих KL і GH знаходяться проекції 3₁, 4₁ конкуруючих точок 3 і 4. Із рис. 2.19, а видно, що точка 3 належить прямій KL, а точка 4 – прямій GH. Точка 3 розташована вище ніж точка 4. Це означає, що пряма KL проходить над прямою GH.

Крім того, одна із проекцій мимобіжних прямих може вироджуватися у точку (рис. 2.19, б). Проекції мимобіжних прямих можуть бути паралельними, якщо прямі належать двом однойменно проекціювальним площинам (рис. 2.19, в).

Дата добавления: 2014-01-07