Теорема сложения вероятностей

1) 0,0006; 2) 0,006; 3) 0,06; 4) 0,01.

1) 0,72; 2) 0,75; 3) 0,79; 4) 0,8.

Тесты

20. Из ящика с 4 белыми и 5 черными шарами вынимают два шара. Какова вероятность, что оба шара белые?

1) 1/4, 2) 1/5, 3) 1/6; 4) 2/9.

21. Что для событий A и B означает соотношение Р (А / В) = P (А)?

1) cобытия A и B зависимы; 2) cобытия A и B независимы; 3) cобытия A и B несовместны; 4) cобытия A и B совместны.

22. Какая из формул соответствует теореме умножения вероятностей?

1 ) Р (А × В) = Р (А) × Р (В / А); 2) Р (А × В) = Р (А) × Р (В); 3) Р (А × В) = Р (А) + Р (В); 4) Р (А × В) = Р (А) × Р (А / В).

23. Кубик брошен 4 раза. Какова вероятность того, что чётное число очков выпало все 4 раза?

1) 1/32; 2) 1/16; 3) 1/8; 4) 1.

24. Какова вероятность того, что взятая наудачу деталь окажется высшего качества, если известно, что 4% всей продукции является браком, а 75% всех не бракованных изделий является продукцией высшего качества?

25. Игральную кость бросают дважды. Какова вероятность того, что ни разу не выпадет цифра 1?

1) 1/6; 2) 1/2; 3) 5/6; 4) 25/36.

26. В магазине имеются три независимо работающих сигнализации. Вероятность того, что в случае ограбления сработает первая сигнализация, равна 0,9, вторая – 0,7, третья – 0,8. Какова вероятность того, что не сработает ни одна сигнализация?

27. В ящике 3 белых и 5 чёрных шаров. Наудачу вынимают шар и возвращают. Затем снова вынимают шарик. Какова вероятность, что оба шара были белыми?

1) 9/64; 2) 9/25; 3) 3/8; 4) 1/4.

Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения, т.е.

Р (А + В) = Р (А) + Р (В) – Р (А × В).

Частные случаи.

1. Для несовместных событий: Р (А + В) = Р(А) + Р(В).

2. Для независимых событий: Р (А + В) = Р (А) + Р (В) – Р (А) × Р (В).

3. Для событий, образующих полную группу Р (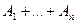) = Р (W) = 1.

4. Для противоположных событий Р () = Р (А) + Р (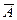) = 1, откуда следует, что Р (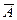) = 1 - Р (А).

Вероятность осуществления хотя бы одного из событий удобнее вычислять по следующей формуле

. (2)

П р и м е р. Вероятность вытащить из колоды, содержащей 52 карты, или короля (А), или трефовую масть (В) равна Р (А + В) = Р (А) + Р (В) – Р (А × В) = 4/52 + 1/4 – 1/ 52 = 4/13. Здесь учтено, что событие А × В – это вытаскивание трефового короля.

Дата добавления: 2014-01-07