Построение их графиков

Исследование поведения функции и

Одной из важнейших прикладных задач дифференциального исчисления является разработка общих приемов исследования поведения функций.

Функция у=f (х) называется возрастающей (убывающей) в неко­тором интервале, если большему значению аргумента из этого интер­вала соответствует большее (меньшее) значение функции, т. Е. при x ₁< x ₂ выполняется неравенство

f (x ₁)< f (x ₂) (f (x ₁)> f (x ₂)).

Перечислим признаки возрастания (убывания) функции.

1. Если дифференцируемая функция у=f (х) на oтрезке [ а; b ] воз­растает (убывает), то ее производная на этом отрезке неотрицательна (неположительна), т. Е. f' (х) 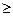0 (f' (х) 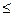0).

2. Если непрерывная на отрезке [ а; b ] и дифференцируемая внутри него функция имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.

Функция y=f (х) называется неубывающей (невозрастающей) в некотором интервале, если для любых x ₁< x ₂ из этого интервала

f (x ₁) 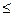f (x ₂) (f (x ₁) 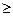f (x ₂)).

Интервалы, в которых функция не убывает или не возрастает, называются интервалами монотонности функций, Характер монотон­ности функции может изменяться только в тех точках ее области опре­деления, в которых меняется знак первой производной. Точки, в которых первая производная функции обращается в нуль или терпит разрыв, называются критическими.

Точка x₁называется точкой локального максимума функции у=f (x), если для любых достаточно малых |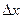|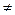0 выполняется нера­венство f (x ₁+ 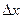) < f (x ₁). Точка x ₂ называется точкой локального ми­нимума функции у=f (х), если для любых достаточно малых |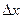|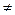0 справедливо неравенство f (x ₂+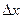)> f (х ₂). Точки максимума и мини­мума называют точками экстремума функции, а максимумы и минимумы функции – ее экстремальными значениями.

Теорема 1 (необходимый признак локального экстремума). Еслифункция. У=f (х) имеет в точке х=х₀ экстремум, то либо f' (х₀) =0, либо f' (х₀) не существует.

В точках экстремума дифференцируемой функции касательная к ее графику параллельна оси Ох.

Теорема 2 (первый достаточный признак локального экстремума). Пусть функция у=f (х) непрерывна в некотором интервале, содержа­щем критическую точку х=х₀ и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки х₀). Если f' (х) при х<х₀ положительна, а при х>х₀ отрицательна, то при х=х₀ функ­ция у=f (х) имеет максимум. Если же f ' (х) при х<х₀ отрицательна, а при х>х₀ положительна, то при х=х₀ данная функция имеет минимум.

Следует иметь в виду, что указанные неравенства должны выпол­няться в достаточно малoй окрестности критической точки х=х ₀. Схема исследования функции у=f (х) на экстремум с помощью первой произ­водной может быть записана в виде таблицы.

Теорема 3 (второй достаточный признак локального экстремума функции). Пусть функция у=f (х) дважды дифференцируема и f' (х₀) =0. Тогда в точке х=х₀ функция имеет локальный максимум, если f» (х₀) <0, и локальный минимум, если f « (х₀) >0.

В случае, когда f» (х₀) =0, точка х= х₀ может и не быть экстремальной..

Лекция 20

Дата добавления: 2014-01-07