Асимтоты

Выпуклость графика функции. Точки перегиба

Кривая, заданная функцией y = f (х), называется выпуклой в ин­тервале (а; b), если все точки кривой лежат не выше любой ее касатель­ной в этом интервале, и вогнутой в интервале (а; b), если все ее точки лежат не ниже любой ее касательной в этом интервале.

Точка кривой М (х₀, f (х₀)) отделяющая выпуклую ее часть от вогну­той, называется точкой перегиба кривой. Предполагается, что в точке М существует касательная.

Теорема 4 (достаточное условие выпуклости (вогнутости) графика функции). Если во всех точках интервала (а;b) вторая производная функции у=f (x) отрицательна (положительна), т. Е. f»(х)<0 (f»(x)>0), то кривая у=f (x) в этом интервале выпукла (вогнута).

В точке перегиба, отделяющей промежуток выпуклости от про­межутка вогнутости, вторая производная функции изменяет свой знак, поэтому в таких точках вторая производная функции или обращается в нуль, или не существует.

Теорема 5 (достаточный признак точки перегиба). Если в точке х = х ₀ f»(х ₀)=0 или f»(х ₀) не существует и при переходе через эту точку производная f»(х) меняет знак, то точка с абсциссой х=х ₀, кривой у=f(x) – точка перегиба.

Лекция 21

Асимптота. Прямая L называется асимптотой данной кривой у=f (x), если расстояние от точки М кривой до прямой L при удалении точки М в беско­нечность стремится к нулю. Из определения следует, что асимптоты
могут существовать только у кривых, имеющих сколь угодно далекие точки («неограниченные» кривые).

Если существуют числа х=x_i (i =1,…, n), при которых 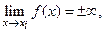т.е. функция имеет бесконечные разрывы, то прямые х=x_i называются вертикальными асимптотами кривой у=f (х). Если существуют пределы

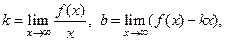
то прямая у=kх+b называется наклонной асимптотой кривой у=f (х) (при k =0 – горизонтальной). При х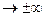 можем прийти к двум значе­ниям для k. Если имеем одно значение для k, то при х 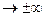можем получить два значения для b.

Лекция 22

Схема исследования функции.

Для полного исследования функции и построения ее графика можно рекомендовать следующую примерную схему:

1) указать область определения функции;

2) найти точки разрыва функции, точки пересечения ее графика с осями координат и вертикальные асимптоты (если они существуют);

3) установить наличие или отсутствие четности, нечетности, периодичности функции;

4) исследовать функцию на монотонность и экстремум;

5) определить интервалы выпуклости и вогнутости, точки перегиба;

6) найти асимптоты графика функции;

7) произвести необходимые дополнительные вычисления;

8) построить график функции.

Лекция 23.

Дата добавления: 2014-01-07