Случайные величины и их числовые характеристики

Если в соответствие случайным событиям полной группы случайных событий поставлены в соответствие некоторые числа, то говорят, что задана случайная величина. Случайные величины в зависимости от того, какой вид имеют множества принимаемых значений делятся на дискретные и непрерывные.

Случайная дискретная величина и ее закон распределения.

Величина называется случайной, если она принимает свои значения в зависимости от исходов некоторого испытания, причем для каждого элементарного исхода оно имеет единственное значеие. Случайная величина называется дискретной, если множество всех возможных значении ее конечно.

Пусть Х – дискретная случайная величина, возможными и единственно возможными значениями которой являются числа х₁,х₂,...,х_n.. Обозначим через р_i=P(X=x_i) (i=1,2,...,n) вероятности этих значений. События X=x_i (i=1,2,...,n), очевидно, образуют полную группу событий, поэтому

р₁+р₂+...+р_n=1.

Определение. Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.

В простейших случаях закон распределения дискретной случайной величины Х удобно задавать таблицей:

Х	х1	х2	...	хn
Р	p1	p2	…	pn

Пример 1. В денежной лотерее разыгрывается 1 выигрыш в 1000 руб., 10 выигрышей по 100 руб. и 100 выигрышей по 1 руб., при общем числе билетов 10000. Найти закон распределения случайного выигрыша Х для владельца одного лотерейного билета.

Здесь возможные значения для Х есть х₁=1000, х₂=100, х₃=1, х₄=0.

Вероятности их соответственно будут

р₁=0,0001, р₂=0,001, р₃=0,01, р₄=1-(р₁+ р₂+ р₃)=0,9889.

Закон распределения для выигрыша Х может быть задан таблицей:

Х
Р	0,0001	0,001	0,01	0,9889

Математическое ожидание.

Определение. Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных ее значений на их вероятности.

Если х₁,х₂,…,х_n есть (полный) набор всех значений дискретной случайной величины Х и р₁,р₂,…,р_n - соответствующие им вероятности, то, обозначая буквой М математическое ожидание, будем иметь

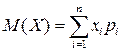(1)

где

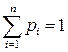(2)

Пример. Найти математическое ожидание выигрыша Х в примере 1.

Решение. Пользуясь помещенной там таблицей, имеем

М(х)= 1000·0,0001+100·0,001+1·0,01+0·0,9889=0,21 (руб)=21 (коп).

Основные свойства математического ожидания.

Теорема 1. Математическое ожидание постоянной величины равно этой постоянной, т.е. если С – постоянна величина, то

М(С)=С.

Теорема 2. Математическое ожидание суммы двух (или нескольких) случайных величин равно сумме математических ожиданий этих величин, т.е. если Х и У – случайные величины, то

М(Х+У) = М(Х)+М(У).

Следствие 1. Если С – постоянная величина, то

М(Х+С)=М(Х)+С

Теорема 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е.

М(ХУ)=М(Х)М(У),

где Х и У – независимые случайные величины.

Следствие 2. Постоянный множитель можно выносить за знак математического ожидания.

Если С – постоянная величина и Х – любая случайная величина, то, учитывая, что С и Х независимы, на основании теоремы 1 получим

М(СХ)=М(С)М(Х)=СМ(Х)

Следствие 3. Математическое ожидание разности любых двух случайных величин Х и У равно разности математических ожиданий этих величин, т.е.

М(Х-У)=М(Х)-М(У).

Дисперсия.

Пусть Х – случайная величина, М(Х) – ее математическое ожидание. Случайную величину Х – М(Х) называют отклонением.

Теорема 1. Для любой случайной величины Х математическое ожидание ее отклонения равно нулю, т.е.

М[Х-М(Х)]=0.

Определение. Дисперсией случайной величины называют называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания.

Отсюда, обозначая дисперсию буквой D, для случайной величины Х будем иметь

D(Х)=М{[Х-М(Х)]²} (3)

Корень квадратный из дисперсии D(Х) называется средним квадратичным отклонением 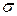этой величины:

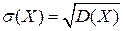(4)

Пример. Пусть закон распределения случайной величины задан таблицей:

Х
Р	¼	1/2	1/4

Определить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратичное отклонение .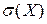

Имеем

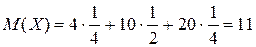
отсюда

и

Теорема 1. Дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом ее математического ожидания, т.е.

D(Х)=М(Х²)-[М(Х)]².

Теорема 2. Дисперсия постоянной величины равна нулю.

Теорема 3. Дисперсия суммы двух независимых случайных величин Х и У равна сумме дисперсий этих величин, т.е.

D(Х+У)=D(Х)+D(У).

Теорема 4. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е.

D(CX)=C²D(X).

Следствие. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин, т.е. если случайные величины Х и У независимы, то

D(X-Y)=D(X)+D(Y)

Лекция 56

Дата добавления: 2014-01-07