Полигон и гистограмма

Эмпирическая функция распределения.

Задачи математической статистики. Выборочный метод.

Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных —.результатов наблюдений.

Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:

а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;

б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого неизвестен.

Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.

Пусть известно статистическое распределение частот количественного признака X. Введем обозначения: n_х—число наблюдений, при которых наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем выборки). Ясно, что относительная частота события X < х равна n_х/n. Если х изменяется, то, вообще говоря, изменяется и относительная частота, т, е. относительная

частота n_х/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события X < х.

Итак, по определению,

F*(x) = n_х/n,

где n_х – число вариант, меньших х; n – объем выборки.

В отличие от эмпирической функции распределения выборки функцию распределения F (х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F (х) определяет вероятность события X < х, а эмпирическая функция F* (х) определяет относительную частоту этого же события. Из теоремы Бернулли следует, что относительная частота события X < х, т. Е. F* (х) стремится по вероятности к вероятности F'{x) этого события. Из определения функции F* (х) вытекают следующие ее свойства:

1) значения эмпирической функции принадлежат отрезку

[0, 1];

2) F* (х) — неубывающая функция;

3) если x_i — наименьшая варианта, то F*(x) = 0 при х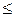х₁, если х₂–наибольшая варианта, то F*(x)= 1 при x>x₂.

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки (х₁; n₁), (x₂; n₂), …, (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, a на оси ординат—соответствующие им частоты n_i. Точки (x_i; n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (х₁; W₁), (х₂W₂), …..., (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат—соответствующие им относительные частоты W_i. Точки (х_i; W_i) соединяют отрезками прямых и получают полигон относительных частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, a высоты равны отношению n_i/h (плотность частоты).

Лекция 58

Параметры распределения.

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Выборочной средней х_в называют среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂,..., х_n признака выборки объема n различны, то

х_в = (х₁ + х₂ + ….+ х_n)/n.

Если же значения признака х₁, х₂ ….. x_k имеют соответственно частоты n₁, n₂ ….. n_k, причем n₁ + …. + n_k = n, то

х_в = (n_{1 *} х₁ + …. + n_k* х_k)/n.

Т. Е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Выборочная средняя, найденная по данным одной выборки, есть, очевидно, определенное число. Если же извлекать другие выборки того же объема из той же генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину, а следовательно, можно говорить о распределениях (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения (его называют выборочным), в частности о математическом ожидании и дисперсии выборочного распределения.

Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения х_в, вводят сводную характеристику— выборочную дисперсию.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения х_в.

Если все значения х₁, х₂,…, х_n признака выборки объема n различны, то

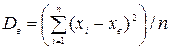
Если же значения признака х₁, х₂,…, х_n имеют соответственно частоты n₁, n₂,…,n_k, причем n₁+ n₂+…+n_k= n, то

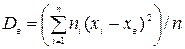
т. Е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

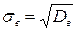
Вычисление дисперсии, безразлично—выборочной или генеральной, можно упростить, используя следующую теорему.

Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:

.

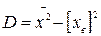Лекция 59

Точечные и интервальные оценки.

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, — точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. Е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами — концами интервала. Интервальные оценки позволяют установить, точность и надежность оценок.

Доверительным называют интервал 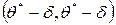, который покрывает неизвестный параметр с заданной надежностью.

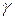Интервал 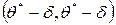имеет случайные концы (их называют доверительными границами). Действительно, в разных выборках получаются различные значения 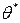. Следовательно, от выборки к выборке будут изменяться и концы доверительного интервала, т. Е. доверительные границы сами являются случайными величинами — функциями от х₁, х₂, …, х_n.

Так как случайной величиной является не оцениваемый параметр в, а доверительный интервал, то более правильно говорить не о вероятности попадания 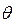в доверительный интервал, а о вероятности того, что доверительный интервал покроет .

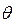Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.

Оценку 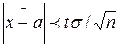называют классической. Из формулы 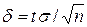, определяющей точность классической оценки, можно сделать следующие выводы:

1) при возрастании объема выборки n число 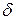убывает и, следовательно, точность оценки увеличивается;

2) увеличение надежности оценки 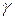приводит к увеличению t (Ф (t) — возрастающая функция), следовательно, и к возрастанию 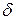; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.

Лекция 60

Дата добавления: 2014-01-07