Доверительный интервал и доверительная вероятность

Наряду с точечными широко применяют интервальные оценки числовых характеристик случайных величин, выражающеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерения. Вероятность того, что погрешность не выйдет за границы некоторого интервала, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс (квантилями), что показано на рис. 1.10.

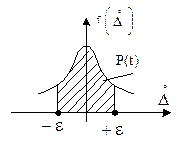
Рис.1.10.

Таким образом, интервал , за границы которого погрешность не выйдет с некоторой вероятностью, называется доверительным интервалом, а характеризующая его вероятность - доверительной вероятностью. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интервалом и по нему определять доверительную вероятность, либо, наоборот, по доверительной вероятности подсчитывать доверительный интервал. Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95 и даже 0,90.

Доверительный интервал обычно выражают через относительную величину 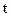в долях среднего квадратического отклонения (“кратность”) 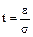. Для нормального закона доверительную вероятность 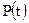определяют по значениям интеграла вероятности (функции Лапласа), который в математической справочной литературе обозначается и определяется

Зная доверительные границы 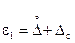и 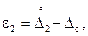можно определить доверительную вероятность

Если значения доверительных границ и симметричны, т.е.

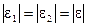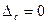, то и .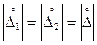

Тогда

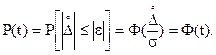
Для наиболее часто встречающихся значений доверительной вероятности в табл. 1.3 указаны соответствующие значения кратности.

Таблица 1.3

P(t)	0,90	0,95	0,99	0,999
t	1,645	1,960	2,576	3,291

При нормальном законе распределения доверительный интервал 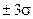имеет доверительную вероятность 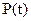=0,9973, что означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше 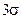. На основании этого основан один из критериев грубых погрешностей, когда остаточная погрешность какого-либо результата измерения превышает значение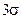 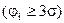, то этот результат считается промахом и исключается из ряда измерений.

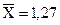
Пример. Для известного числа измерений получены значения и . Определить вероятность того, что имеет место неравенство 1,26<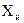<1,28.

Так как , то 0,01/0,025=0,4. Используя таблицу интеграла вероятности, находим 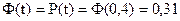. Следовательно, около 30% общего числа измерений будут иметь случайную погрешность , не превышающую ±0,01.

Дата добавления: 2014-01-07