Стационарная теория теплового воспламенения

Два типа воспламенения

Для того, чтобы началось горение, необходимо создать определенные начальный условия в системе - воспламенить или зажечь смесь. Опыт указывает на возможность двоякого способа воспламенения.

Первый способ заключается в том, что смесь вся целиком доводится до такой температуры, выше которой она самостоятельно, без внешнего воздействия, воспламеняется. Второй способ состоит в том, что холодная смесь зажигается только в какой-либо одной точке пространства посредством какого-либо высокотемпературного источника (обычно это искра, накаленное тело, постороннее пламя) и дальнейшее воспламенение объема газа происходит затем без внешнего вмешательства, самопроизвольно.

Соответственно этим двум способам воспламенения говорят о самовоспламенении и о вынужденном воспламенении, зажигании. Характеристики обоих процессов различны, но в основе предполагается действие одного общего фактора – теплового.

При рассмотрении вопроса о воспламенении возможны два подхода:

1. Стационарный - определяются условия (критически»), при которых стационарное течение процесса становится невозможным -происходит переход от плавного развития реакции в взрывному.

2. Нестационарный - исследуется зависимость химической реакция и изменения температуры от временя и определяется индукционный период. Кроме статических режимов воспламенения (когда температура стенок реакционного сосуда считается постоянной),, возможно рассмотрение также динамических режимов с переменной температурой стенки. Динамические теории теплового самовоспламенения смыкается с теориями зажигания - при увеличении темпа нагрева вещество не успевает прогреваться целиком, и процесс протекает в режиме зажигания в ограниченной области.

Д.А. Франк - Каменецкий наиболее строго рассмотрел вопрос осуществимости установившихся режимов при чисто кондуктнвном отводе тепла. Результаты эти пригодны для гомогенного твердого топлива, для расчета газовых систем при низких давлениях, для быстро развивающихся процессов, когда за время индукционного периода предвзрывной разогрев системы не столь значителен. В теории Д.А. Франк - Каменецкого рассматривается стационарное в тепловом отношении состояние системы (теплоотвод равен теплоприходу) и ищутся условия, при котором оно невозможно.

Д.А. Франк - Каменецкий предложил следующее решение задачи. Пусть все тепло, выделявшееся за счет химической реакции, теряется через стенки при помощи кондукции. Теплопроводность стенок принимается бесконечно большой, температура стенок поддерживается постоянной. Предполагается, что за время установления стационарного равновесия изменение начальной концентрации реагирующих веществ невелико, поэтому диффузией компонентов пренебрегают. В этих условиях ищется стационарное состояние системы.

Рассмотрим простейшую задачу стационарной теория, а именно - тепловой взрыв в плоском реакционном сосуде толщиной 2r _t В этом случае уравнение (I.I6) примет вид

lDT+QW= . (2.11)

Для решения уравнения (2.II) представим его в безразмерной форме. Безразмерную температуру примем согласно формуле (I.3I), при этом Т_i= Т_о, т.е. температуре стенки. Для определения безразмерной координаты введем характерную длину l представляющую собой параметр, определяемый отношением теплоты, отводимой посредством теплопроводности, к теплу, выделяемому в химии ческой реакции:

. (2.12)

Тогда безразмерная координата f=x/l и отсчитывается от центра сосуда. Применяя преобразование Д.А. Франк-Каменецкого, приведем уравнение (2.II) к форме

(2.13)

и определим граничные условия

f = 0; dQ/dT = 0; Q = 0 (2.14.)

f = f_o = r_o/l; Q = 0 (2.15)

В данном случае предполагается стационарное состояние, когда температура в центре сосуда равна температуре стенки (график Q= Q (f)) изобразится в этом случае прямой линией, параллельной оси абсцисс).

Из постановки задачи в безразмерных переменных видно, что характер решения и условия его существования зависят лишь от одного параметра - безразмерной толщины x _o. При малых f_o, когда велик теплоотвод в стенки сосуда, решение существует, а при больших x _{o ,}, когда условия приближаются, к адиабатическим, - решения нет. Следовательно, должно существовать критическое значение x_крит., разделяющее область существования и не существования решения. Это критическое значение x _(крит) определяет критический размер сосуда 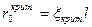, а при заданных размерах сосуда - критическую температуру теплового взрыва.

Интегрирование уравнения (2.13) легко выполняется, если ввести переменную 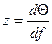. Тогда

,

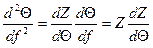и уравнение припишет вид

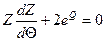(2.16)

откуда с учетом условия Z = 0, q = 0 следует:

(2.17)

(знак минус перед корнем выбран из тех соображения, что при дальнейшей процессе температура должна уменьшаться по мере удаления от центра сосуда). Интегрируя выражение (2.17) еще pas, получим: 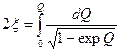(2.18)

или, пронимая . будем иметь

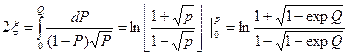(2.19)

Выражение (2.19) можно преобразовать:

или окончательно получим частное решение:

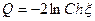(2.20)

Дальнейшие рассуждения проведем на основе группового подхода, разработанного Г.И. Баренблаттом (1959). Можно убедиться, что уравнение (2.13) с граничным условием (2,15) инвариантно относительно некоторой однопараметрической группы преобразований. Действительно, пусть 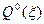)- некоторое частное решение (.2.13), удовлетворявшее условию (2.15). Тогда при любом постоянном d данное выражение

Q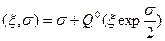 (2.21)

также удовлетворяет выражению (2.13) с условием (2.15). Пользуясь группой (2.21), можно по одному частному решению (2.20) построить всю совокупность решений с различной температурой Qc. пр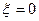и и 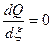. Можно также найти огибающую однопараметрического семейства всех решений уравнения (2,13), удовлетворяющих условию (2.14). Дифференцируя выражение (2,21) по параметру группы d, полагая 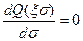, обозначен учитывая, что 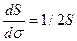, находим

. (2.22)

Соотношение (2.22) с учетом, что частное решение Q (S) имеет вид выражения (2.20), переходят в уравнение 1-SthS=0. (2.23)

Функция SthS - четная относительно S, обращается в О при S = 0 и монотонно растет с ростом S>0. Поэтому уравнение (2.23) имеет единственный корень; вычисление дает S=So =1,2.

Подставляя в (2.21) d, выраженное через So, находим с учетом частного решения (2.20) уравнение огибающей

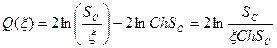(2.24).

Критический размер сосуда определяется из условия равенства температуры стенки и центра сосуда (Q=0)

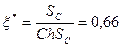
или .

Предвзрывной разогрев в центре сосуда равен

;

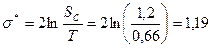
и отношение перепада температуры в центре сосуде и на стенке к абсолютной температуре стенки составляет

(2.27)

Поскольку RTo/E по условию << I, то величина DT/T_o мала. Это оправдывает применение преобразования Д.А. Франк - Каменецкого.

Дата добавления: 2014-01-07