Тепловая теория зажигания

Первая постановка задачи о зажигании принадлежит Я.Б. Зельдовичу /1,3/, который обобщил в 1939 г. стационарную теорию {валового взрыва на случай плоскопараллельного сосуда с различными температурами стенок и нашел критическое условие воспламенения в такой системе.

Рассмотрим это решение. Если взять для простоты сосуд с бесконечными плоскими стенками, то при условии, когда одна стенка нагрета до некоторой температуры Те. а другая поддерживается при начальной температуре, в сосуде будет определенное стационарное распределение температур до тех пор, пока температура Те превысит некоторую критическую величину. Переход к зажиганию определяется моментом, когда градиент (а соответственно, dQ/dz ) около стенки становится > 0. Для рассмотрения этого вопроса вернемся к уравнению (2.13):

Обратимся к семейству интегральных кривых этого уравнения.

Ограничиваясь кривыми, максимум которых лежит при 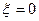, получим картину, представленную на рисунке 2.7. Чем выше максимум кривой, тем она круче в соответствии с большим значением и тем больше производная температуры вдали от максимума, так как больше количество отводимого тепла.

Рис. 2.7. Семейство интегральных кривых уравнения (2.13)

Если теперь сдвинуть кривые таким образом, чтобы все они пересекались а начале координат, то получим распределение температур, изображенное на рисунке 2.8, при этом граничное условие на нагретой стенке примет вид

Q = 0 при (2.41)

Риc. 2.8. Стационарные распределения температуры вблизи накаленной плоской

поверхности

Сравнивая два рисунка, можно утверждатъ, что наименее круто спадает и, следовательно, выше всех остальных кривых, на большом удаления от стенки располагается кривая, дня которой точка с координатами Q = 0 является максимумом (кривая I). Действительно, кривая 2 с положительной производной температуры у стенки достигает максимума при 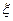>0. Кривую 3, у которой производная в начале координат отрицательна, можно рассматривать как продолжение кривой, имевшей максимум слева, при 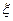<0. Поэтому кривые 2 и 3 должны спадать более круто при больших 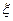по сравнению с кривой 1. Таким образом, кривая I, отвечающая решению с нулевой производной на горячей стенка, при больших 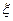асимптотически стремятся к огибающей и задает предельную зависимость расстояние-температура холодной стенки на пределе воспламенения.

Таким образом, при больших расстояниях между стенками, когда температуре одной значительно больше температуры другой, задача сводится к решению уравнения (2.13) с граничный условием (2,41) на горячей стенке и условием

, (2.42) вдали от нее, здесь - безразмерный теплоотвод от зоны химической реакции в холодный газ.

Интегрируя выражение (2.13) получим

, где . Обозначим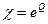

, . (2.43)

С₁ - константа интегрирования; знак «минус» выбираем из условия убывания Q с увеличением ξ. Интегрируем еще раз, с учетом выражения 2.41,

; ; .

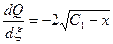Тогда получаем уравнение .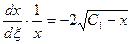

Разделяем переменные .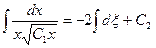

Для взятия интеграла с правой стороны проведем еще одну замену:

; ; ;

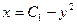. (2.44)

Применим метод разбиения на элементарные дроби:

= . (2.45)

Из граничного условия (2.41) определим постоянную интегрирования

. И окончательно получаем решение (2.13) в неявном виде:

или

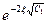= .(2.46)

Для получения явной зависимости представим постоянную интегрирования С₁ в виде гиперболической функции 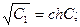С₁ = 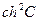и соответственно перепишем уравнение (2.46):

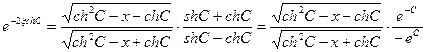или

. (2.47)

Откуда получаем:

Возведем в квадрат и заменим 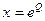и получим решение уравнения (2.13) в форме

. (2.48.)

Анализируя кривые рисунка 2.8, видим, что при больших значениях , когда выделившееся тепло успевает отводиться в холодные слои газа, существует два решения: одно устойчивое с отрицательной производной и одно неустойчивое с положительной производной. При малых решения нет. Следовательно, должно быть критическое значение теплоотвода, при котором решение задачи существует. Это наименьшее значение дается условием касания интегральной кривой с огибающей на бесконечности (при ). При приближении к критическим условиям кривые с максимумом в положительной области 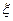и без максимума сближаются и сливаются в одну. Вычислим теплоотвод, используя решение(2.48) 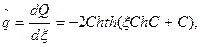₍₂.₄₉₎

который при равен Минимум достигается при с=0 и равен

= 2

или в размерных переменных

(2.52)

Очевидно, что решение стационарного уравнения не позволяет непосредственно рассчитать основную характеристику процесса - время задержки зажигания. Однако полученные Я.Б. Зельдовичем результаты имели большое значение для дальнейшего развития теории. В ней, в частности, были обоснованы важнейшие отличительные особенности процесса зажигания:

- рассмотрение модели полубесконечного пространства;

- пренебрежение скоростью тепловыделения за счет химической реакции при начальной температуре вещества Т _о (по сравнению со скоростью тепловыделения при температура зажигания Т с).

Для расчета характеристик зажигания и анализа зависимости их от исходных параметров необходимо рассматривать нестационарную картину развития процесса. Система уравнений (1.23, 1.25) в нестационарной тепловой теории зажигания учитывает гомогенную экзотермическую реакцию и нестационарную теплопроводность без учета возможных физических и химических факторов, осложняющих явление (фвзовые превращения, многостадийность, диспергирование и другое). Поскольку аналитического решения эта система не имеет, для анализа закономерностей процесса в каждом частном случав используют либо числвнные расчеты на ЭВМ, либо приближенно-аналитические методы.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Какая связь существует между температурой и концентрацией исходного реагента в процессах горения?

2. Сформулируйте определение двух типов воспламенения. Можно ли их строго разграничить?

3. Почему в стационарной задаче о тепловом воспламенении можно не вводить уравнение диффузии?

4. Укажите границы применения преобразования Д.А. Франк-Камвнецкого.

5. Нарисуйте и объясните диаграмму Н.Н. Семенова.

6. Сформулируйте задачу о зажигании плоской стенкой и запишите исходное уравнение и граничные условия.

Дата добавления: 2014-01-07