Нестационарная теория теплового взрыва

Лекция

Эта теория была разработана Н.Н. Семеновым в 1940 г.

Рассмотрим простую систему. Пусть некоторый объем газа заключен в сосуд, стенки которого неизменно поддерживаются при заданной температуре Т_о. Предположим, что при реакции температура внутри сосуда везде одинакова и равна Т. Ввиду этого вся разница температур между газом и стенкой сосредоточена на границе между ними. Соответственно этому внутри сосуда в газе не существует различия в концентрациях реагирующих веществ.

Напишем два выражения - для скорости выделения тепла во всем объеме V и для отдачи тепла через стенки сосуда. Если тепловой эффект реакции равен Q Дж/моль, то скорость выделения тепла в сосуде„ содержащей V объемов газа, равна

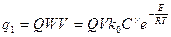(2.28)

Это тепло идет частично на нагревание газа, частично теряется через стенки сосуда. Количество потерянного тепла запишем в виде

q₂ =aF(T-To),

где F - общая поверхность стенок сосуда.

Предположение, что внутри сосуда температура однородна, означает, что скорость выравнивания температур там очень велика, так что основное термическое сопротивление оказывает тонкий слой газа, прилегающий к стенкам сосуда; понятно, что в этом случае величина a зависит как от формы и размеров сосуда, так и от температуры. Построим графики зависимости тепловыделения и теплоотвода от температуры (рис.2.3). Предположим, что до момента. воспламенения в сосуде не происходит изменения реагирующих веществ, т.о. концентрация постоянна и равна начальной Со. Система кривых 1,2,3 соответствует скорости выделения тепла для трех различных скоростей реакции (уравнение 2.21). Прямая 4 соответствует скорости отдачи тепла в зависимости от температуры внутри сосуда (2.29).

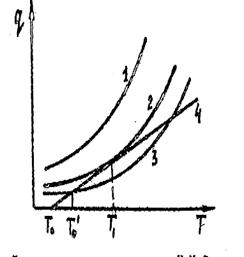
Рис.2.3. Диаграмма теплового взрыва Н.Н. Семенова: 1,2,3-тепловыделение;

4-теплоотвод

Когда реакция идет по кривой 3, то смесь будет разогреваться от Т₀ до Т₁, так как до этого момента теплоприход превышает теплоотвод. В точке Т₁ нагрев прекратится. И система придет в равновесие. Реакция пойдет дальше с постоянной скоростью. Если количество реагирующих молекул не будет меняться, практически скорость будет падать.

В случае, когда реакция описывается кривой 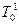тепловыделение всегда превышает теплоотвод, и система с самого начала непрерывно наращивает температуру. Скорость реакции быстро возрастает, что ведет к явлению взрыва.

Существует, очевидно, определенное условие, характеризующее переход от ограниченного роста температуры к неограниченному. Это условие реализуется для кривой 2. В этом случае произойдет возрастание температуры газа до величины Т₁.

Начиная с этого момента система находится в равновесии. Но если равновесие в точке Т₁ для кривой 3 было устойчивым (повышение Т о только несколько изменяло Т₁) то равновесие Т₄ явно неустойчиво. Небольшие флуктуации температуры приводят к превышению теплоприхода над теплоотводом и к прогрессивному саморазогреву системы.

Условием перехода системы к воспламенению является условие касания кривой теплоотвода к кривой тепловыделения. В этой точке имеет место равенство скоростей тепловыделения и теплоотвода.

q₁=q₂ 2.30),

и равенство скоростей изменения этих количеств с температурой

(2.31)

Эти два условия однозначно определяют величину T₁, характеризующую для данной системы предельное условие воспламенения, и температура T₁ носит название температуры воспламенения или самовоспламенения горючей смеси. Найдем критические условия теплового взрыва, т.е. значения параметров системы на границе между двумя возможными режимами протекания процесса - стационарной медленной реакцией н взрывом.

Кинетика процесса описывается уравнением

.

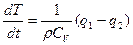Представим его в безразмерном виде. Для этого, кроме безразмерного времени 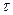и температуры Q введем параметр æ -- -критерий Н.Н. Семенова

æ = ,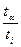

где 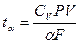- характерное время теплоотвода;

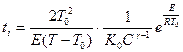период индукции адиабатической реакции

В этом случае уравнение (2.30) можно представить в следующем виде

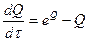/æ (2.30).

с печальными условиями 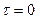, Q=0.

Решения уравнения (2.31) имеет вид (О.М.Тодес) /3/

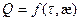, æ =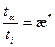=const, (2.32)

т.е. зависит oт одного безразмерного параметра, критическое значение которого необходимо определить. При достаточно больших æ характерной время теплоотдачи намного больше характерного времени тепловыделения, и тепло не успевает отводиться в стенки сосуда, должен произойти взрыв. В уравнении (2.31) это проявляется в том, что при достаточно больших æ. правая часть уравнения положительна при любых Q, т.е. уравнение

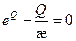(2.33)

не имеет корней 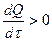при всех t - температура смеси нeограниченно увеличивается. Если æ имеет такое значение, что корни уравнения (2.33) вещественны, то возможен стационарный режим - температура сначала возрастает, но только до такого значения, при котором 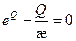обращается в нуль, а далее реакция идет при постоянной температуре.

Условие теплового взрыва (рис.2.3) можно записать как условие касания функции expQ и Q/æ при некоторой температуре Q = Q*, а именно:

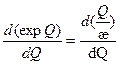; (2.34)

и в этом случае условия воспламенения принимают: вид

Q*=1; æ*=1/l (2.35).

Решение (2.35) можно записать так:

T* - T₀ =;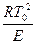

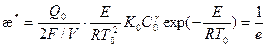(2.36).

Существенным в теории Н.Н. Семенова является то, что к анализу нестационарного процесса применен стационарный подход, а именно: условия взрыва формулируется как условие исчезновения стационарного режиме (невозможность протекания медленной реакции с тепловыделением, уравновешенным теплообменом). Численные расчеты с высокой точностью подтверждают исходные предпосылки и выводы теории Н.Н. Семенова:

- предвзрывной разогрев равен (в пределах порядка) характеристическому интервалу ;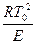

- выгорание смеси за период индукции мало, и им можно пренебречь: 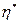<<1.

Из приведенных расчетов можно сделать еще один важный вывод. Прологарифмировав выражение (2.36), получаем:

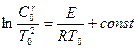. (2.37)

В частности, для бимолекулярной реакции в газовой фазе 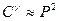и тогда

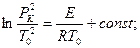(2.38)

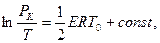
где через Pk обозначено давление, соответствующее критическому условию самовоспламенения.

Это соотношение, которое называется соотношением Н.Н. Семенова, устанавливает связь между Рк и Т_о на границе, В системе координат Рк и Т_о эта зависимость дает кривую, ограничивающую область взрыва (рис.2.4). Аналогичные зависимости можно установить между составом смеси и температурой при постоянном - давлении, а также между критическим давлением и составом смеси при постоянном значении Т₁ (практически ~Т_О).

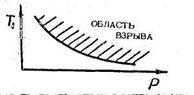
Рис.2.4. Зависимость температуры воспламенения Tj м давления Р при заданном постоянном начальном составе смеси

2.5. Тепловой взрыв в динамических условиях /4/

Рассмотренное случая соответствуют постоянству температуры стенки, равной начальной температуре смеси Тс = То=const. В работах А.Г. Мержанова с сотрудниками развита теория теплового взрыва в условиях линейного изменения To (нагрев и охлаждение), основанная на решении системы уравнений- (1.23)-(1.25), дополненных законом изменения температуры окружающей среда:

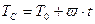:, (2.39)

где 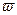- скорость изменения температуры.

При нагреве (при To<<T*, где Т* - критическая температура теплового взрыва в статических условиях) система ведет себя сначала как инертное вещество, и температура в ней стационарно запаздывает по сравнению с Тс. В дальнейшем начинает проявляться тепловыделение от реакции, и запаздывание исчеза­ет, а температура в системе обгоняет температуру в окружающей среде. 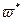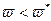Для реакции нулевого порядка тепловой взрыв неизбежен, В реальных системах из-за выгорания вещества существует критическое значение скорости нагрева (при ) реакция протекает спокойно с небольшим перегревом, при 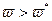реакция завершается тепловым взрывом). Вблизи 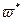существует область квазистационарного протекания химической реакции, характеризующиеся большими глубинами предвзрывного превращения вещества 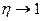к вырождением самого теплового взрыва (рис.2.5).

В динамических режимах вместо То удобно использовать критическую температуру Т*. Основным параметром динамической задачи является отношение характерных времен изменения температуры и химической реакции U:

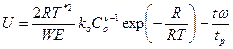(2.40)

и представляет собой по существу динамический аналог критериев Н.Н. Семенова и Д.А. Франк - Каменецкого.

Рис. 2.5. Зависимость T (Ts) при различных значащих параметра U

2 .6. Вынужденное воспламенение (зажигание)

Под вынужденным воспламенением (зажиганием) понимают случаи воспламенения, когда основная масса горючей среды остается холодной, а нагревание производится только в одном небольшом по объему участке среды, газа в частности. Это может быть осуществлено разнообразными способами: введением в среду накаленного тела, небольшим пламенем, электрической искрой того или иного тала и так далее. С точки зрения физической сущности процесса вынужденного зажигания, нет принципиальных отличий от процесса самовоспламенения, поскольку условия самоускорения реакций в данном случае также существенны, но их действие пространственно ограничивается лишь частью объема горючей смеси. С точки зрения расчета, явление это более сложно, чем самовоспламенение.

Видимым и практически удобным критерием зажигания является факт распространения пламени от местного источника воспламенения на весь объем среды. Поэтому факторы, определяющие критические условия в случае зажигания, должны быть связаны, с одной стороны, со свойствами источника зажигания и, с другой- с условиями распространения горения, распространения пламени.

Для того, чтобы представить себе механизм зажигания от накаленного тела, рассмотрим высказанные в связи с этим соображения В. Вант-Гоффа.. Процессом диффузии пренебрегаем, считая, что концентрация реагирующих веществ везде одинакова и равна начальной. Предположим, что на поверхности тела произошло повышение температуры до некоторой величины Т_1. В сpeде инертной, неспособной к реакции, распределение температура изобразится кривой T₁А₁ „ Для аналогичного процесса в реакционноспособной среде кривая температур должна быть уже несколько иной в силу дополнительного выделения тепла реакция,и ее можно изобразить примерно в вида пунктирной линии 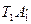. Повысим теперь начальную температуру тела до Т₂,.В инертной среде это поведет к возникновению распределения температуры Т₂А₂ подобного предыдущему с более резким ее спадом. В реагирующей среде; напротив; в силу увеличивающегося с повышением температуры выделения тепла, кривая температур будет падать медленнее, чем кривая 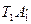и можно предвидеть, что найдется такая температура Т₂, при которой понижение температуры, по крайней мере вблизи источника, не произойдет, и кривая температур примет вид 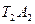. Если после этого повысить начальную температуру источника, то стационарное состояние станет невозможным, так как температура в окружающей среде начнет прогрессивно возрастать по мере удаления от источника до тех пор, пока не произойдет воспламенения ( Т₃--В) (рис.2.6). Температура Т₂ является для этих условий критической предельной температурой, т.е. температурой зажигания, и по своему смыслу аналогична температуре воспламенения в случае процессов самовоспламенения.

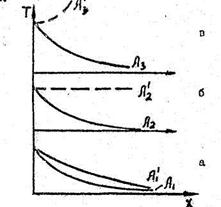
Рис. 2.5. Распределение температуры в процессе зажигания

Дата добавления: 2014-01-07