Постановка основных начально-граничных задач

Вывод уравнения колебаний струны.

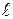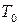Рассмотрим натянутую вдоль оси струну длины , закрепленную на концах. Пусть к концам струны приложены вдоль оси силы натяжения , равные по величине, но противоположные по направлению. Под струной понимается тонкая, упругая, гибкая нить. Тонкая – это значит, мы отвлекаемся от двух физических измерений струны, которые считаются бесконечно малыми по сравнению с длиной струны. Гибкая – это значит, что струна не оказывает никакого сопротивления изменению ее формы, не связанному с изменением ее длины. Математически это будет означать, что силы натяжения 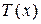, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю.

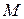Если теперь выведем струну из положения равновесия и подвергнем действию внешней силы, то струна начнет колебаться, при этом точка струны, занимавшая при равновесии положение к моменту времени займет положение (см. рис. 1).

Для вывода уравнения колебаний струны сделаем ряд предположений относительно рассматриваемых колебаний:

1) колебания являются поперечными, т.е. все точки струны движутся перпендикулярно оси только в одной плоскости;

2) колебания малы;

3) пренебрегаем действием силы тяжести.

Рис.1

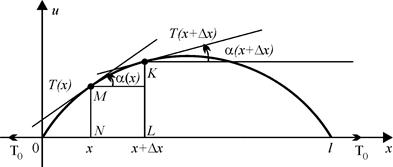
Рис. 1

Поскольку струна колеблется в одной плоскости, то закон ее колебаний, т.е. смещение 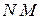задается одной функцией двух переменных 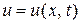где 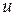– отклонение точки с абсциссой от положения равновесия до точки 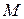в момент времени . Если колебания малы, то это значит, что функция 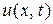мала и при достаточной гладкости струны – тангенс угла наклона касательной к струне в точке в момент времени тоже мал.

Предположим, что колебания настолько малы, что можно пренебречь квадратом , т.е.

.

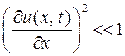Отсюда следует, что длина струны при малых колебаниях остается неизменной. В самом деле, длина дуги 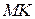в момент времени определяется по формуле

.

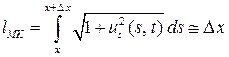Поскольку не происходит удлинения участков струны в процессе малых колебаний, то по закону Гука величина натяжения не зависит ни от времени, ни от и во всех точках одно и тоже, и равно .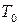

Перейдем к выводу уравнения колебаний струны. Для этого выделим малый участок струны 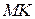и спроектируем все действующие силы на этот участок на оси координат. Согласно принципу Даламбера, сумма проекций всех сил, включающая силы инерции в момент времени , должна равняться нулю.

Сумма проекций сил натяжений на горизонтальную ось равна

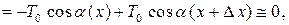
так как

.

Сила тяжести струны не учитывается, так как полагается, что сила натяжения 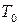настолько значительна, что можно пренебречь действием силы тяжести.

Рассмотрим проекцию сил натяжения на вертикальную ось:

.

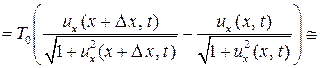
Отсюда на основании теоремы Лагранжа, имеем

.

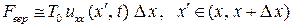Поскольку рассматриваем поперечные вынужденные колебания, то силы инерции и внешние силы направлены параллельно оси . Найдем их проекции на ось . Пусть 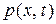– непрерывная внешняя сила, рассчитанная на единицу длины. Тогда ее проекция на ось приближенно равна

.

Пусть – непрерывная линейная плотность струны, тогда масса участка струны 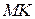приближенно равна

.

Сила инерции по закону Ньютона определяется

.

Тогда проекция всех сил на ось равна

.

Сократив на 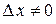последнее равенство и перейдя к пределу при 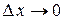, получим уравнение вынужденных колебаний струны

. (1)

Если струна однородная, то и уравнение (1) запишется в виде

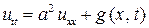, (2)

где , .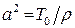

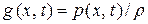Если отсутствуют внешние силы, т.е. 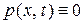, то уравнение (2) примет вид

. (3)

Уравнение (3) называют уравнением свободных колебаний однородной струны.

Продольные колебания стержня, а также колебания газа в трубке сводятся к уравнению вида (1).

Дата добавления: 2014-01-07