
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П.1. Решение задачи Дирихле в круге
|
|
|
|
Решение задачи Дирихле для уравнения Лапласа
в круге методом разделения переменных. Формула Пуассона
Рассмотрим уравнение Лапласа
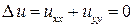 (1)
(1)
в круге  с границей
с границей  (см. рис. 4).
(см. рис. 4).
Задача Дирихле. Найти в области  функцию
функцию  , удовлетворяющую следующим условиям:
, удовлетворяющую следующим условиям:
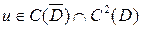 , (2)
, (2)
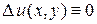 ,
, 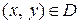 , (3)
, (3)
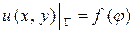 ,
, 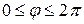 , (4)
, (4)
где  – заданная достаточно гладкая функция,
– заданная достаточно гладкая функция, 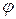 – угол между осью
– угол между осью  и радиусом-вектором
и радиусом-вектором 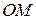 ,
,  .
.
Для решения поставленной задачи (2) – (4) применим метод разделения переменных. В дальнейшем будем предполагать, что функция  на сегменте
на сегменте  непрерывна и имеет на этом сегменте непрерывную первую производную, т.е.
непрерывна и имеет на этом сегменте непрерывную первую производную, т.е. 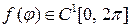 .
.

Рис. 4
В области  перейдем к полярным координатам
перейдем к полярным координатам  ,
,  ,
,  ,
, 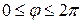 . Тогда уравнение (1) в полярных координатах имеет вид
. Тогда уравнение (1) в полярных координатах имеет вид
 . (5)
. (5)
Решение  уравнения (5) будем искать в виде произведения двух функций
уравнения (5) будем искать в виде произведения двух функций
 в
в  . (6)
. (6)
Подставив выражение (6) в уравнение (5), получим
 .
.
Поделив на  , имеем
, имеем
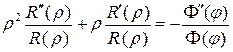 . (7)
. (7)
Левая часть равенства (7) зависит только от 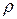 , а правая только от
, а правая только от 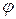 . Поэтому равенство (7) возможно только тогда, когда левая и правая части представляют собой одну и ту же константу
. Поэтому равенство (7) возможно только тогда, когда левая и правая части представляют собой одну и ту же константу 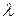 . Тогда уравнение (7) распадается на два обыкновенных д.у.:
. Тогда уравнение (7) распадается на два обыкновенных д.у.:
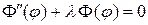 , (8)
, (8)
 . (9)
. (9)
Поскольку  , то из (6) следует, что
, то из (6) следует, что  , т.е. функция
, т.е. функция 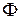 является периодической с периодом
является периодической с периодом  . Это возможно только в том случае, когда
. Это возможно только в том случае, когда 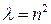 ,
,  и общее решение д.у. (8) определяется по формуле
и общее решение д.у. (8) определяется по формуле
 ,
,
где 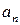 и
и 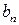 – произвольные постоянные.
– произвольные постоянные.
Уравнение (9) при 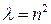 имеет два линейно независимых решения
имеет два линейно независимых решения
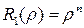 ,
,  .
.
Поскольку ищется непрерывное в 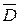 решение, то в качестве решения уравнения (9) следует взять функцию
решение, то в качестве решения уравнения (9) следует взять функцию  . Тогда на основании (6) найдем
. Тогда на основании (6) найдем
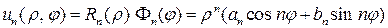 .
.
Таким образом, найдены частные решения уравнения (5) в круге  , которые являются гармоническими в
, которые являются гармоническими в  при каждом
при каждом  .
.
Если  , то решением уравнения (5) является функция
, то решением уравнения (5) является функция 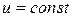 . Для удобства возьмем
. Для удобства возьмем 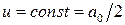 , тогда решение задачи Дирихле в круге
, тогда решение задачи Дирихле в круге  будем искать в виде суммы
будем искать в виде суммы
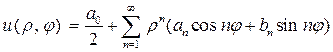 . (10)
. (10)
Пусть последовательности 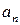 и
и 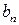 ограничены. Обозначим через
ограничены. Обозначим через 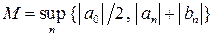 . Тогда ряд (10) при любых
. Тогда ряд (10) при любых  , где
, где 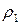 – фиксированное положительное число, мажорируется сходящимся числовым рядом
– фиксированное положительное число, мажорируется сходящимся числовым рядом
 .
.
Тогда на основании признака Вейерштрасса ряд (10) сходится равномерно на любом замкнутом круге  . Поэтому сумма ряда (10) непрерывна на замкнутом круге
. Поэтому сумма ряда (10) непрерывна на замкнутом круге  . Отсюда в силу произвольности числа
. Отсюда в силу произвольности числа 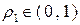 следует, что функция
следует, что функция 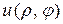 непрерывна в круге
непрерывна в круге  .
.
Ряд (10) внутри круга  допускает почленное дифференцирование по переменным
допускает почленное дифференцирование по переменным 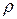 и
и 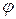 любое число
любое число 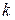 раз, так как полученные при этом ряды для всех
раз, так как полученные при этом ряды для всех  мажорируются сходящимися числовыми рядами типа (11).
мажорируются сходящимися числовыми рядами типа (11).
Действительно, из ряда (10) формальным почленным дифференцированием 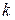 раз составим ряды:
раз составим ряды:
 , (11)
, (11)
 . (12)
. (12)
Ряд (11) при  мажорируется сходящимся числовым рядом
мажорируется сходящимся числовым рядом
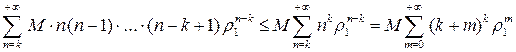 .
.
А ряд (12) оценивается также сходящимся числовым рядом
 .
.
Следовательно, ряды (11) и (12) равномерно и абсолютно сходятся в замкнутом круге  . Поэтому суммы рядов (11) и (12) непрерывны в
. Поэтому суммы рядов (11) и (12) непрерывны в  .
.
Если теперь подставить ряды, полученные из (11) при  и
и 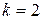 и ряд (12) при
и ряд (12) при 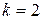 в уравнение (5), то убеждаемся, что функция
в уравнение (5), то убеждаемся, что функция 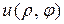 , определенная рядом (10), является его решением внутри круга
, определенная рядом (10), является его решением внутри круга  .
.
Таким образом, ряд (10) внутри круга  является гармонической функцией. Пусть ряд (10) сходится равномерно на замкнутом круге
является гармонической функцией. Пусть ряд (10) сходится равномерно на замкнутом круге 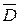 . Тогда удовлетворяя ряд (10) граничному условию (4), получим
. Тогда удовлетворяя ряд (10) граничному условию (4), получим
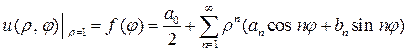 . (13)
. (13)
Ряд (12) представляет собой разложение в ряд Фурье функции  на промежутке
на промежутке  . Тогда коэффициенты
. Тогда коэффициенты 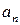 и
и 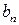 определяются по формулам:
определяются по формулам:
 ,
,  , (14)
, (14)
 ,
, 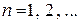 . (15)
. (15)
Если функция  непрерывна на сегменте
непрерывна на сегменте  и имеет там непрерывную первую производную, то ряд (13) равномерно сходится на сегменте
и имеет там непрерывную первую производную, то ряд (13) равномерно сходится на сегменте  к самой функции
к самой функции  , при этом ряд (13) мажорируется сходящимся числовым рядом
, при этом ряд (13) мажорируется сходящимся числовым рядом
 . (16)
. (16)
Поскольку для любого 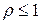 ряд (10) мажорируется рядом (16), то на основании признака Вейерштрасса ряд (10) равномерно и абсолютно сходится на
ряд (10) мажорируется рядом (16), то на основании признака Вейерштрасса ряд (10) равномерно и абсолютно сходится на 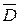 . Тем самым доказана следующая теорема.
. Тем самым доказана следующая теорема.
Теорема 1. Если функция 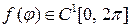 и
и 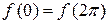 , то существует единственное решение задачи Дирихле в круге
, то существует единственное решение задачи Дирихле в круге  , которое определяется рядом (10). Коэффициенты
, которое определяется рядом (10). Коэффициенты 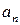 и
и 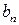 ряда (10) находятся соответственно по формулам (14) и (15).
ряда (10) находятся соответственно по формулам (14) и (15).
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1075; Нарушение авторских прав?; Мы поможем в написании вашей работы!