Правило Верещагина

При определении перемещений по теореме Максвелла – Мора приходится составлять аналитические выражения подынтегральных функций изгибающих моментов и производить интегрирование.

В 1925 г. студент Московского института железнодорожного транспорта А. Н. Верещагин предложил простой графоаналитический способ вычисления интеграла Мора. Этот способ получил название способа Верещагина.

Интеграл Мора имеет вид:

,

где M_x – это выражение изгибающего момента от заданной нагрузки, в числе которой может быть и распределенная нагрузка.

Следовательно, эпюра этого момента может быть криволинейной. В то же время функция 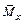представляет собой выражение изгибающего момента от единичной нагрузки, которая может быть либо силой, либо моментом. В этом случае эпюра 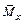всегда прямолинейна.

Рассмотрим некоторый участок балки жесткостью EI_z = const, в пределах которого функции изгибающих моментов M_x и 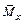непрерывны (рис. 19.4.1).

Обозначим площадь эпюры M_x (рис. 19.4.1, а) на участке – ω; угол наклона эпюры 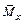к оси х – α (рис. 19.4.1, б).

На расстоянии x от начала участка (рис. 19.4.1, а) выделим элементарный участок . Тогда .

В этом же сечении на эпюре (рис. 19.4.1, б) .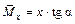

Подставив полученные выражения в интеграл Мора (19.1.1), имеем:

, (19.4.1)

но интеграл – это статический момент площади эпюры М относительно оси z.

В соответствии с (8.1.3) имеем

, (19.4.2)

где – площадь эпюры ; – расстояние от начала участка до центра тяжести эпюры .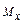

Выражение (19.4.1) имеет вид , но из рис. 19.4.1, б видно, что 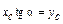, где y_C – ордината эпюры , расположенная над центром тяжести эпюры M_x.

Окончательно правило Верещагина имеет вид:

(19.4.3)

Искомое перемещение равно произведению площади эпюры моментов от заданной нагрузки на расположенную под её центром тяжести ординату единичной эпюры , поделенное на жесткость.

Этот способ вычисления перемещений называют способом перемещения эпюр.

Следует отметить, что способ Верещагина может применяться лишь в тех случаях, когда:

а) жесткость каждого участка постоянна;

б) ось балки прямолинейна.

Порядок определения перемещений способом Верещагина:

1. Построить эпюру изгибающих моментов M_x от заданной нагрузки.

2. Отбросить мысленно всю заданную нагрузку, и к сечению, перемещение которого требуется определить, приложить соответствующую искомому перемещению единичную силу.

3. Построить эпюру изгибающих моментов от единичной нагрузки.

4. Вычислить площади ω _i эпюры изгибающих моментов от заданной нагрузки для каждого участка l_i, в пределах которого функции M_x и 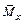являются непрерывными.

Рис. 19.4.2  

5. Умножить площади ω _i на соответствующие ординаты эпюры изгибающих моментов от единичной нагрузки (ордина-ты берутся под центрами тяжести площадей ω _i).

6. Сложить полученные результаты и разделить на жесткость EI_z..

Знаки величин ω _i и определяются знаками эпюр изгибающих моментов. Если эпюра M_x имеет сложный вид, то она может быть разбита на простые фигуры (табл. 19.4.1), при этом каждую из полученных площадей умножают на ординату единичной эпюры под ее центром тяжести и результаты суммируют.

Таблица 19.4.1

Форма площади эпюры	Площадь эпюры	Абсцисса центра тяжести площади
1.
2. Парабола 2 ^ой степени
3. Парабола 2 ^ой степени
4. Парабола 2 ^ой степени

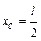
Пример 19.4.1. Определить изгиб сечения А (рис. 19.4.2, а), если EI_z= const.

Решение. Построим эпюру M_x от заданной нагрузки (рис. 19.4.2, б).

Отбросим заданную нагрузку и в т. А приложим силу 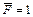(рис. 19.4.2, в) и построим эпюру изгибающих моментов от этой силы (рис. 19.4.2, г).

Определим площадь эпюры M_x:

.

Под центром тяжести эпюры M_x определим ординату на эпюре (табл. 19.4.1):

.

Тогда по правилу Верещагина:

.

Пример 19.4.2. Определить угол поворота сечения А (рис. 19.4.3, а), если EI_z = const.

Решение. Построить эпюру M_x от заданной нагрузки (рис. 19.4.3, б). Отбросим заданную нагрузку и в т. А приложим единичный момент = 1 (рис. 19.4.3, г).

Площадь эпюры :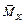

.

Под центром тяжести эпюры M_x определим ординату y_c на эпюре 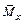: , тогда

.

Площади простейших фигур и положение их центров тяжести приведены в табл. 19.4.1.

Дата добавления: 2014-01-07