Расчеты при изгибе

Рассмотрим балку прямоугольного поперечного сечения (рис. 27.3.1). В сечениях этой балки возникают только изгибающие моменты, т. е. имеет место деформация чистого изгиба.

Напряжения в произвольном сечении можно определить по формуле:.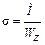

Если изгибающий момент в сечении меньше опасного момента М_у, то эпюра напряжений в опасном сечении имеет вид (рис. 27.3.2, а).

Вначале с увеличением нагрузки нормальные напряжения во всех сечениях балки будут возрастать. Затем при некотором значении М в крайних точках опасного сечения наибольшие нормальные напряжения достигают предела текучести. При этом сохраняется линейный закон изменения напряжений (рис. 27.3.2, б).

При увеличении нагрузки напряжения в крайних волокнах достигнут предела текучести – 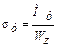(рис. 27.3.2, б), а величина изгибающего момента достигнет опасного значения – М = М_у

В таком состоянии балка оказывается работоспособной, т. к. для ее разрушения требуется дальнейшее увеличение нагрузки, хотя при расчете по допускаемым напряжениям это состояние считается опасным, так как напряжения в опасных точках достигли предела теку­чести.

При дальнейшем увеличении нагрузки напряжения в крайних точках, достигнув предела текучести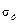, не увеличиваются, хотя деформации растут по всему сечению.

Дальнейший рост деформаций приводит к росту напряжений только во внутренних точках сечения, у которых нормальные напряжения меньше 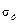. При этом у краев балки образуется зона с напряжениями 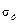, и эпюра напряжений принимает вид двух трапеций (рис. 27.3.2, в).

Последующее увеличение нагрузки сопровождается ростом зоны с напряжениями 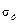, которая в предельном состоянии занимает все сечения, и эпюра напряжений получает вид двух прямоугольников (рис. 27.3.2, г).

Сечение, в котором напряжения по всей высоте равны 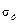, т. е. в котором эпюра напряжений имеет вид двух прямоугольников, называют пластическим шарниром, а нагрузку, вызвавшую пластический шарнир, – предельной нагрузкой. При возникновении пластического шарнира балка становится неработоспособной, т. е. она превращается в механизм и поэтому теряет несущую способность.

Определим величину предельного момента.

Выделим элементарную площадку на расстоянии у₁ в сжатой зоне (рис. 27.3.3), тогда в предельном состоянии на эту площадку действует элементарная сила 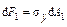, момент этой силы относительно нейтральной линии равен .

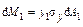Площадку 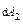возьмем в растянутой зоне, тогда

,

.

Определим предельный момент:

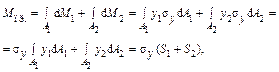
где 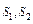– статические моменты соответственно сжатой и растянутой зон относительно нейтральной линии.

Обозначим 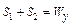, где W_у – осевой пластический момент сопротивления. Тогда

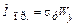. (27. 3.1)

Продольная сила в поперечном сечении при чистом изгибе равна нулю, поэтому площади сжатой и растянутой зон равны, т. е. нейтральная ось в сечении, совпадающем с пластическим шарниром, делит поперечное сечение на две равновеликие части. Поэтому при несимметричном поперечном сечении нейтральная ось в предельном состоянии не проходит через центр тяжести сечения.

Определим пластический момент сопротивления для прямоугольного сечения:

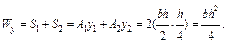
Осевой момент сопротивления прямоугольного сечения

,

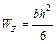тогда

,

т. е. пластический момент сопротивления в 1,5 раза больше осевого, значит, предельный момент в опасном сечении равен

.

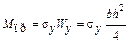Опасный момент в том же сечении равен

,

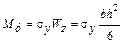значит,

,

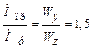т. е. предельный момент при расчете по методу разрушающих нагрузок оказался в 1,5 раза больше предельного момента при расчете по допускаемым напряжениям. При других формах поперечного сечения это различие может быть еще больше.

Пример. Определить предельное значение нагрузки q, действующей на балку (рис. 27.3.5), если считать материал идеально упруго-пластичным, . Размеры поперечного сечения даны в см.

Решение. Построим эпюру моментов для заданной балки (рис. 27.3.6, а). Предельный момент в опасном сечении равен

,

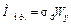где , .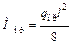

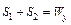Для определения пластического момента сопротивления необходимо определить положение нейтральной линии в предельном состоянии из условия равенства площадей сжатой и растянутой зон:

Проведем случайную ось z (рис. 27.3.6, б), тогда

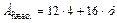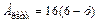, , т. е.

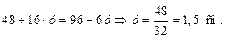
Определим статические моменты сжатой и растянутой площадей относительно нейтральной линии:

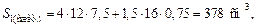
Пластический момент сопротивления

W_у = 378 + 162 = 540 см³ ,

тогда

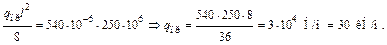
Дата добавления: 2014-01-07