Вероятность гипотез. Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий В₁, В₂, В₃,…. В_n,образующих полную группу.

Поскольку заранее неиз­вестно, какое из этих событий наступит, их называют гипотезами.

Вероятность появления события А опреде­ляется по формуле полной вероятности (см. 2-ой учебный вопрос):

Допустим, что произведено испытание, в результате которого появилось событие А.Поставим своей задачей определить, как изменились (в связи с тем, что собы­тие А уже наступило ) вероятности гипотез. Другими словами, будем искать условные вероятности

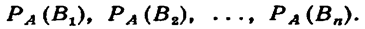
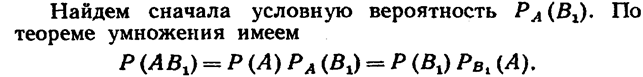
Отсюда

Заменив здесь Р (А) по формуле (*). получим

Аналогично выводятся формулы, определяющие услов­ные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы В_i (i = 1, 2, …, n) может быть вычислена по формуле:

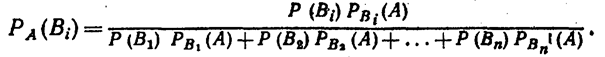
Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.).

Формулы Бейеса позволяют переоценить вероятности гипотез после того, как ста­новится известным результат испытания, в итоге кото­рого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Веро­ятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму—0,4. Вероятность того, что годная деталь будет приз­нана стандартной первым контролером, равна 0,94, а вторым—0,98. Годная деталь при проверке была признана стандартной.Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предполо­жения (гипотезы ):

1) деталь проверил первый контролер (гипотеза В₁);

2) деталь проверил второй контролер (гипотеза B₂).

Искомую вероятность того, что деталь проверил первый контролер, найдем по Формуле Бейеса:

По условию задачи имеем:

Искомая вероятность

Как видно, до испытания вероятность гипотезы В₁ равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала рав­ной 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятностьрассматриваемой гипотезы.

Дата добавления: 2014-01-07