Теорема сложения вероятностей совместных событий

Была рассмотрена теорема сложения для несов­местных событий. Здесь будет изложена теорема сложения для совместных событий.

Два события называют совместными если появление одного из них не исключает появления другого в одном и том же испытании.

Пример 1. А—появление четырех очков при бросании играль­ной кости; В—появление четного числа очков. События А и В— совместные.

Пусть события А и В совместны, причем даны веро­ятности этих событий и вероятность их.совместного по­явления. Как найти вероятность события А+В, состоя­щего в том, что появится хотя бы одно из событий А и В? Ответ на этот вопрос дает теорема сложения вероят­ностей совместных событий.

Теорема.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Доказательство. Поскольку события А и В, по условию, совместны, то событие А + В наступит, если наступит одно из следующих трех несовместных событий:

Событие А произойдет, если наступит одно из двух несовместных событий:

А B¯ или А В. По теореме сложения вероятностей несовместных событий имеем

Отсюда

Аналогично имеем

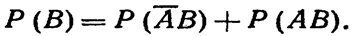
Отсюда

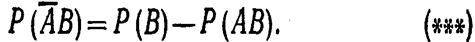
Подставив (**) и (***) в (*), окончательно получим

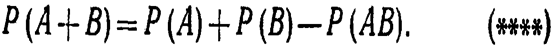
Замечание 1. При использовании полученной формулы сле­дует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми.

Для независимых событий

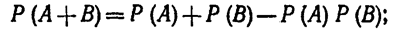
Для зависимых событий

Замечание 2. Если события А и В несовместны, то их сов-

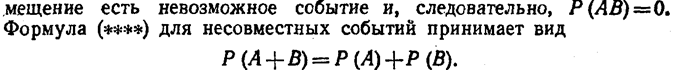
Мы вновь получили теорему сложения для несовместных собы­тий.

Таким образом, формула (****) справедлива как для совмест­ных, так и для несовместных событий.

Пример 2. Вероятности попадания в цель при стрельбе первого

вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому собы­тия А (попадание первого орудия) и В (попадание второго орудия) независимы.

Вероятность события АВ (оба орудия дали попадание)

Искомая вероятность

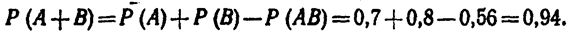
Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой Р=1—

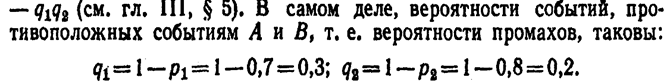
Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна

Как и следовало ожидать, получен тот же результат.

2.Формула полной вероятности

Пусть событие А может наступить при условии появления одного из несовместных событий В₁,В_2, ..., Вn (гипотез), которые образуют полную группу. Пусть известны вероятности этих событий (Р(В_i)и условные вероятности Р_В1(А), Р_В2(А),… Р_Вn(А) события А. Как найти вероятность события А? Ответ на этот вопрос дает следующая теорема.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несо­вместных событий B₁ B₂,...,Вп образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероят­ность события А:

Эту формулу называют «формулой полной вероятности».

Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий В_1, B_2,..., В_п. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В₁А, В₂А_, В₃А,….., В_ПА.

Пользуясь для вычисления вероятности события А теоремой сложе­ния. Для несовместных событий получим

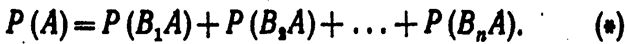
Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем

Подставив правые части этих. равенств в соотноше­ние (*), получим формулу полной вероятности

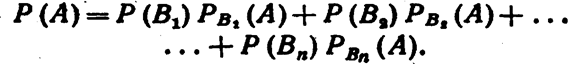
Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго—0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора)—стандартная.

Решение. Обозначим через А событие «извлеченная деталь стандартна».

Деталь может быть извлечена, либо из первого набора (событие В₁), либо из второго (событие В₂).

Вероятность того. что деталь вынута из первого набора.

Р(В₁)=1/2.

Вероятность того, что деталь вынута из второго набора.

Р(В₂)=1/2.

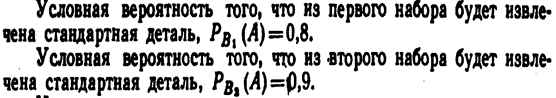
Искомая вероятность того, что извлеченная наудачу деталь-стандартная, по формуле полной вероятности равна

Дата добавления: 2014-01-07