Независимых событий

Теоремы умножения для зависимых и

Рассмотрим два события: А и В; пусть вероят­ности Р(А) и Р_А(В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.

Теорема. Вероятность совместного появления двух событии равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предпо­ложении, что первое событие уже наступило:

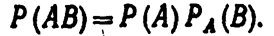
Доказательство. По определению условной веро­ятности.

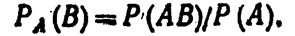
Отсюда

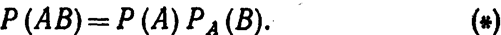
Замечание.

Применив формулу (*) к событию ВА, получим

или, поскольку событие ВА не отличается от события АВ,

Сравнивая формулы (*) и (**), заключаем о справедливости ра­венства

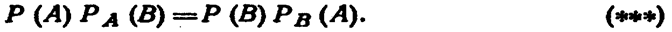
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появи­лись:

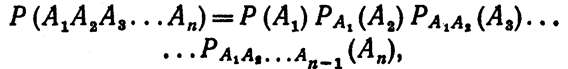
Заметим, что порядок, в котором расположены собы­тия, может быть выбран любым, т.е. безразлично какое событие считать первым, вторым и т. д.

Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков.Сборщик взял один валик, а затем второй. Найти вероят­ность того, что первый из взятых валиков—конусный, а второй— эллиптический.

Решение. Вероятность того, что первый валик окажется ко­нусным событие А),

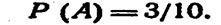
Вероятность того, что второй валик окажется эллиптическим (событие в), вычисленная в предположении, что первый валик—. конусный, т. е- условная вероятность

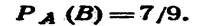
По теореме умножения, искомая вероятность

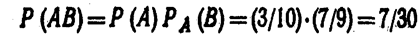
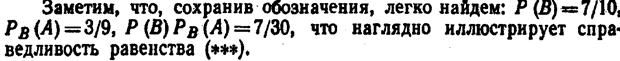
Пример 2. В урне 5 белых,.4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не воз­вращая его обратно.Найти вероятность того, что при первом испы­тании появится белый шар (событие А), при втором—черный (собы­тие В) и при третьем—синий (событие С).

Решение.Вероятность появления белого шара в первом испытании

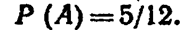
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность

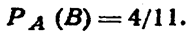
Вероятность появления синего шара в третьем испытании, вы­численная в предположении, что в первом испытании появился белый шар, а во втором—черный, т. е. условная вероятность

Искомая вероятность

Независимые события. Теорема умножения для независимых событий

Пусть вероятность события В не зависит от по­явления события А.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

Подставив (*) в соотношение (***) предыдущего подвопроса лекции, получим

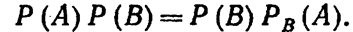
Отсюда

т. е. условная вероятность события А в предположении, что наступило событие В, равна его безусловной вероят­ности. Другими словами, событие А не зависит от со­бытия В.

Итак, если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.

Для независимых событий теорема умножения

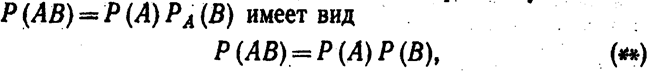
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Равенство (**) принимают в качестве определения не­зависимых событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависи­мыми.

На практике о независимости событий заключают по смыслу задачи.

Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» неза­висимы.

Пример 1. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (собы­тие А) равна 0,8, а вторым (событие В)—0,7.

Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность

Следовательно,

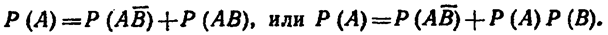
Отсюда

т. е. события А и В независимы.

Несколько событий называют попарно независимыми» если каждые два из них независимы.

Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.

Для того чтобы обобщить теорему умножения на не­сколько событий, введем понятие независимости событий в совокупности.

Несколько событий называют независимыми в совокуп­ности (или просто независимыми), если независимы ка­ждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если со-

события независимы в совокупности, то условная вероят­ность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие собы­тия из числа остальных, равна, его безусловной вероят­ности.

Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.

Поясним сказанное на примере. Пусть в урне имеется 4 шара, окрашенные: один—в красный цвет (А), один— в синий цвет (В), один—в черный цвет (С) и один—во все эти три цвета (АВС). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет?

Так как из четырех шаров два имеют красный цвет, то Р (А) == 2/4 =1/2. Рассуждая аналогично, найдем Р(В)==1/2, Р (С) = 1/2. Допустим теперь, что взятый шар имеет синий цвет, т. е. событие В уже произошло. Изме­нится ли вероятность того, что извлеченный шар имеет красный цвет, т. е. изменится ли вероятность события А? Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события А по-преж­нему равна 1/2. Другими словами, условная вероятность события А, вычисленная в предположении, что наступило событие В, равна его безусловной вероятности. Следова­тельно, события А и В независимы. Аналогично придем к выводу, что события А и С, В и С независимы. Итак, события А, В и С попарно независимы.

Независимы ли эти события в совокупности? Оказы­вается, нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероят­ность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице.

Приведем теперь следствие из теоремы умножения.

Следствие.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

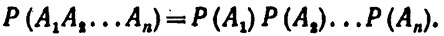
Доказательство. Рассмотрим три события: А, В и С. Совмещение событий А, В и С равносильно сов­мещению событий АВ и С.

Поэтому

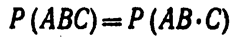
Так как события А, В и С независимы в совокуп­ности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух неза­висимых событий имеем:

Итак. окончательно получим

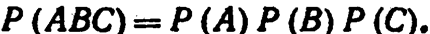
Для произвольного «п» доказательство проводится ме­тодом математической индукции.

независимы в совокупности. '

Пример 2. Найти вероятность совместного появления герба при одном бросании двух монет.

Решение. Вероятность появления герба первой монеты (событие А) -

Вероятность появления герба второй монеты (событие В)

События А и В независимые, поэтому искомая вероятность по теореме умножения равна

Дата добавления: 2014-01-07