
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема сложения вероятностей несовместных событий
|
|
|
|
Теоремы сложения вероятностей несовместных событий и событий, образующих полную группу событий
Пусть события А и В—несовместные!!!, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие А, либо событие В? Ответ на этот вопрос дает теорема сложения.
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Доказательство. Введем обозначения: п— общее число возможных элементарных исходов испытания; т1 -число исходов, благоприятствующих.событию А;m2— число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
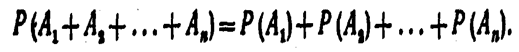
Доказательство. Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий. А, В и С, равносильно наступлению одного из двух событий, А+В и С, поэтому в силу указанной теоремы

Для произвольного числа попарно несовместных событий доказательство проводится методом математической индукции.
Пример 1. В урне 30 шаров: 10 красных, 5 синих я 15 белых. Найти вероятность появления цветного шара,
Решение. Появление цветного шара означает появление либо краевого, либо синего шара.
Вероятность появления красного шара (событие А)
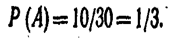
Вероятность появления синего шара (событие В)

События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.
Искомая вероятность
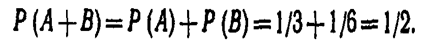
Пример 2. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую—0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
Решение. События А—«стрелок попал в первую область» и В— «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.
Искомая вероятность
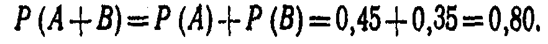
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1133; Нарушение авторских прав?; Мы поможем в написании вашей работы!