Виды случайных событий

События называют несовместными, если появле­ние одного из них исключает появление других событий в одном и том же испытании.

Пример 1. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась не­стандартная деталь»—несовместные.

Пример 2. Брошена монета. Появление «герба» исключает по­явление надписи. События «появился герб» и «появилась надпись» — несовместные.

Несколько событий образуют полную группу, если в результате испытания появится, хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несов­местны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.

Пример 3. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий:

«выигрыш выпал на первый.билет и не выпал на второй», «выигрыш не выпал на первый билет и выпал на второй», «выигрыш выпал на оба билета», «на оба билета выигрыш не выпал». Эти события обра­зуют полную группу попарно несовместных событий.

Пример 4. Стрелок произвел выстрел по цели. Обязательно прои­зойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.

События называют равновозможными, если есть осно­вания считать, что ни одно из них не является более возможным, чем другое.

Пример 5. Появление «герба» и появление надписи при бросании монеты—равновозможные события. Действительно, предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не оказывает влияния на выпадение той или иной стороны монеты.

Пример 6. Появление того или иного числа очков на брошенной игральной кости—равновозможные события. Действительно, предпо­лагается, что игральная кость изготовлена из однородного материала, имеет форму правильного многогранника и наличие очков не оказы­вает влияния на выпадение любой грани.

3. Классическое и статистическое определение вероятности. Основные формулы комбинаторики

3.1 Классическое определение вероятности.Свойства вероятности.

Чтобы количественно сравнивать между собой событияпо степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие.Такое число и назовают вероятностью события.

Таким образом, мы вводим в рассмотрениевторое основное поня­тие теории вероятностей — понятие вероятности события.

Вероятность события есть численная мера степени объективной возможности этого события.

Заметим, что уже при самом введении понятия вероятности со­бытия мы связываем этим понятием определенный практический смысл, а именно: на основании опыта мы считаем более вероятными те события, которые происходят чаще; менее вероятными — те события, которые происходят реже; мало вероятными—те, которые почти ни­когда не происходят.

Таким образом, понятие вероятности события в самой своей основе связано с опытным, практическим понятием частоты события.

Вероятность — одно из основных понятий теории вероятностей.Существует несколько определений этого понятия. Приведем определение, которое называют клас­сическим. Далее укажем слабые стороны этого определе­ния и приведем другие определения, позволяющие пре­одолеть недостатки классического определения.

Рассмотрим пример. Пусть в урне содержится 6 оди­наковых, тщательно перемешанных шаров, причем 2 из них—красные, 3—синие и 1—белый. Очевидно, возмож­ность вынуть наудачу из урны цветной (т. е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли.охарактеризовать эту возможность числом? Оказывается, можнo. Это число и называют вероятностью события (появления цветного шара). Таким образом, В ероятностьесть число, характеризующее степень воз­можности появления события.

Отношение числа благоприятствующих событию А элементарных исходов к общему числу называют вероятностью события А и обозначают через 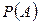. Следовательно,вероятность того, что, взятый шар окажется цветным, равна 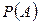=5/6. Это число и даёт количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь классическое определение вероятности.

Вероятностью события Аназывают отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. И так, вероятность события А определяется формулой:

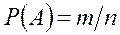
где m—число элементарных исходов, благоприятствую­щих А; п— число всех возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы не­совместны, равновозможны и образуют полную группу.

Из классического определения вероятности вытекают следующие её свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае m = n, следовательно,

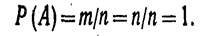
Свойство 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

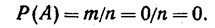
Свойство 3.Вероятность случайного события есть положительное число, заключенное между нулем и еди­ницей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 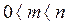, значит, 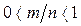, следовательно:

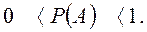
Итак, вероятность любого события удовлетворяет двой­ному неравенству

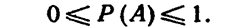
Далее приведены теоремы, которые позволяют по из­вестным вероятностям одних событий находить вероятно­сти других событий.

Замечание 1.Современные строгие курсы теории вероятностей построены на теоретико-множественной основе.

Пусть в результате испытания наступает одно и только одно из

Получено классическое определение вероятности.

Замечание 2.Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятно­сти.

В системе аксиом, предложенной А. Н. Колмогоровым, неопре­деляемыми понятиями являются элементарное событие и вероятность. Приведем аксиомы, определяющие вероятность:

1. Каждому событию А поставлено в соответствие неотрицатель­ное действительное число Р (А). Это число называется вероятностью события А.

2. Вероятность достоверного события равна единице:

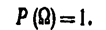
3. Вероятность наступления хотя бы одного из попарно несов­местных событий равна сумме вероятностей этих событий.

Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем.

3.2 Относительная частота. Устойчивость относительной частоты

Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.

Относительной частотой событияназывают отноше­ние числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.

Таким образом, относительная частота события А опре­деляется формулой

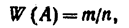
где т — число появлений события, п — общее число испы­таний.

Сопоставляя определения вероятности и относитель­ной частоты, заключаем:определение вероятности не требует, чтобы испытания производились в действитель­ности; определение же относительной частоты предпола­гает, что испытания были произведены фактически.Дру­гими словами, вероятность вычисляют до опыта, а относительную частоту—после опыта.

Пример I. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей.

Отно­сительная частота появления нестандартных деталей

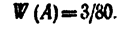
Пример 2. По цели произвели 24 выстрела, причем было зареги­стрировано 19 попаданий.

Относительная частота поражения цели:

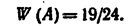
Длительные наблюдения показали, чтоесли в одина­ковых условиях производят опыты, в каждом из которых число испытаний достаточно велико,то относительная частота обнаруживает свойство устойчивости. Это свой­ство состоит в том, что в различных опытах относитель­ная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого по­стоянного числа. Оказалось, что это постоянное число есть вероятность появления события.

Таким образом,если опытным путем установлена от­носительная частота, то полученное число можно принять за приближенное значение вероятности.

Проиллюстрируем свойство устойчивости на примерах.

Пример 3. По данным шведской статистики, относительная час­тота рождения девочек за 1935 г. по месяцам характеризуется сле­дующими числами (числа расположены в порядке следования меся­цев, начиная с января): 0,486; 0,489; 0,490; 0.471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0.482; 0,473

Относительная частота колеблется около числа 0,482, которое можно принять за приближенное значение вероятности рождения девочек.

Заметим, что статистические данные различных стран дают при­мерно то же значение относительной частоты.

Пример 4.Многократно проводились опыты бросания монеты, в которых подсчитывали число появления «герба». Результаты не­скольких опытов приведены в табл. 1.

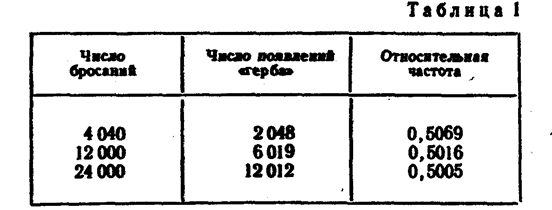Здесь относительные частоты незначительно отклоняются от чис­ла 0,5, причем тем меньше, чем больше число испытаний. Например, при 4040испытаниях отклонение равно 0.0069, а при 24000 испытаний - лишь 0,0006.

Приняв во внимание, чтовероятность по­явления «герба» при бросании монеты равна 0,5, мы вновь убеж­даемся, что относительная частота колеблется около вероятности.

3.3 Ограниченность классического определения вероятности. Статистическая вероятность.

Классическое определение вероятности предпо­лагает, что число элементарных исходов испытания ко­нечно.На практике же весьма часто встречаются испы­тания,число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность Классического определения.

Наиболее слабая сторона классического определениясостоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий.

Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания говорят из соображений симметрии. Так, например, пред­полагают, что игральная кость имеет форму правильного многогранника (куба) и изготовлена из однородного мате­риала.Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко.По этой причине наряду с классическим опреде­лением вероятности используют и другие определения, в частности статистическое определение вероятности: в качестве ста­тистической вероятности события принимают относи­тельную частоту или число, близкое к ней.

Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0,4, то это число можно принять за статистиче­скую вероятность события.

Легко проверить, что свойства вероятности, вытекаю­щие из классического определения, сохраняются и при статистическом определении вероятности.

1).Действи­тельно, если событие достоверно, то т = п и относитель­ная частота

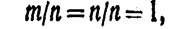
т. е. статистическая вероятность достоверного события (так же как и в случае классического определения) равна единице.

2). Если событие невозможно, то m = 0 и, следовательно, относительная частота

0/0=0,

т. е. статистическая вероятность невозможного события равна нулю.

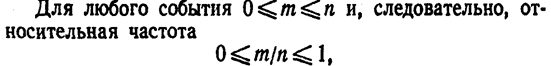3).

т. е. статистическая вероятность любого события заклю­чена между нулем и единицей.

Для существования статистической вероятности собы­тия А требуется:

а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает;

б ) устойчивость относительных частот появления А в различных сериях достаточно большого числа испыта­ний.

Недостатком статистического определения является - неоднозначность статистической вероятности. Так, в при­веденном примере, в качестве вероятности события можно принять не только 0.4, но и 0,39; 0,41 и т. д.

Дата добавления: 2014-01-07