Полная группа событий

Теорема.Сумма вероятностей событий А1, А2.... А_n, образующих полную группу, равна единице:

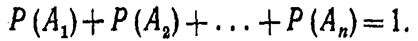
Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность досто­верного события равна единице, то

(*)

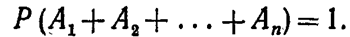Любые два события полной группы несовместны, поэтому можно применить следствие теоремы сложения нескольких попарно несовместных событий:

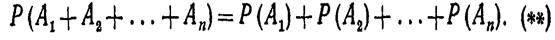
Сравнивая левые и правые части уравнений (*) и (**), можно записать

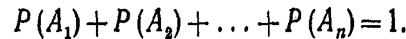
Пример. Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность полу­чения пакета из города А равна 0,7, из города В-— 0,2. Найти веро­ятность того, что очередной пакет будет получен из города С.

Решение. События «пакет получен из города А», «пакет получен из города В», «пакет получен из города С» образуют полную группу,

поэтому сумма вероятностей этих событий равна единице:

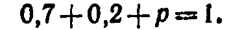
Отсюда искомая вероятность

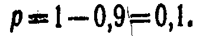
3. Теорема сложения вероятностей противоположных событий. Принцип практической невозможности маловероятных событий.

3.1 Противоположные события

Противоположными называют два единственно возможных события, образующих полную группу.

Если одно из двух противоположных событий обозначено через А, то другое принято обозначать .

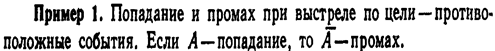
Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь»—противо­положные.

Теорема сложения вероятностей противоположных событий.

Теорема. Сумма вероятностей противоположных собы­тий равна единице:

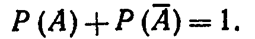
Доказательство.Противоположные события об­разуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице (см. п.п. 2.2),

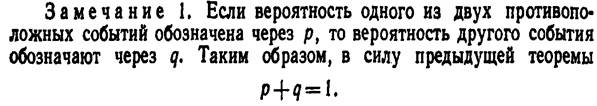
Пример 3. Вероятность того, что день будет дождливым, р==0,7. Найти вероятность того, что день будет ясным.

Решение. События «день дождливый» и «день ясный»—про­тивоположные, поэтому искомая вероятность

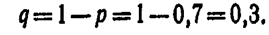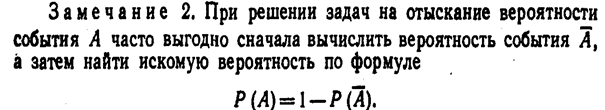
Очевидно»

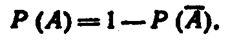
Искомая вероятность

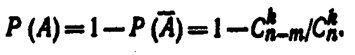
3.2. Принцип практической невозможности маловероятных событий

При решении многих практических задач прихо­дится иметь дело с событиями, вероятность которых весьма мала, т. е. близка к нулю. Можно ли считать, что маловероятное событие А в единичном испытании не произойдет? Такого заключения сделать нельзя, так как не исключено, хотя и мало вероятно, что событие А наступит.

Казалось бы, появление или непоявление маловероят­ного события в единичном испытании предсказать невоз­можно. Однако длительный опыт показывает, что мало­вероятное событие в единичном испытании в подавляющем большинстве случаев не наступает. На основании этого факта принимают следующий «принцип практической невозможности маловероятных событий»: если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это собы­тие не наступит.

Естественно возникает вопрос: насколько малой должна быть вероятность события, чтобы можно было считать невозможным его появление в одном испытании? На этот вопрос нельзя ответить однозначно. Для задач, различных по существу, ответы разные. Например, если вероятность того, что парашют при прыжке не раскроется, равна 0,01, то было бы недопустимым применять такие парашюты. Если же вероятность того, что поезд дальнего следования прибудет с опозданием, равна 0,01, то можно практически быть уверенным, что поезд прибудет вовремя.

Достаточно малую вероятность, при которой (в дан­ной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заклю­ченные между 0,01 и 0,05 (или 1-5%). Уровень значимости, равный 0,01, называют однопроцентным; уровень значимости, равный 0,02, называют двухпроцентным, и т. д.

Подчеркнем, что рассмотренный здесь принцип позво­ляет делать предсказания не только о событиях, имею­щих малую вероятность, но и о событиях, вероятность которых близка к единице.

Из принципа невозможности маловероятных событии вытекает следующее важное для приложений следствие: если слу­чайное событие имеет вероятность, очень близкую к еди­нице, то практически можно считать, что в единичном испытании это событие наступит. Разумеется, и здесь ответ на вопрос о том, какую вероятность считать близ­кой к единице, зависит от существа задачи.

Введем еще одно важное понятие:понятие о независимых и зависимых событиях.

Событие А называется независимым от события В, если вероят­ность события А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если вероят­ность события А меняется в зависимости от того, произошло собы­тие В или нет.

Рассмотрим примеры.

1) Опыт состоит в бросании двух монет; рассматриваются события:

А — появление герба на первой монете, В — появление герба на второй монете.

В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А н е з а в и с и м о от собы­тия В.

2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события:

А—появление белого шара у 1-го лица, В — появление белого шара у 2-го лица.

Вероятность события А до того, как известно что-либо о событии В, равна 2/3. Если стало известно, что событие В произошло, то вероятность события А становится равной 1/2, из чего заключаем, что событие А зависит от события В.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А/В) или Р_В(А).

Для условий последнего примера

Условие независимости события А от события В можно записать в виде:

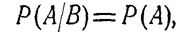
а условие зависимости—в виде:

----------------------------------------------------------------------------------------

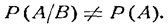
Другое определение условной вероятности: Условной вероятностью Р_А(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероят­ность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность

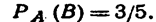
Этот же результат можно получить по формуле

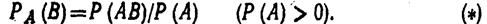
Действительно, вероятность появления белого шара при первом ис­пытании

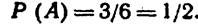
Искомая условная вероятность

(*)

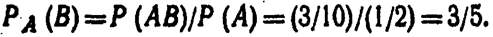Как видим, получен прежний результат.

Исходя из классического определения вероятности, формулу (*) можно доказать. Это обстоятельство и служит основанием для следующего общего (применимого не только для классической вероятности) определения условной вероятности.

Общее определение условной вероятности:

Условная вероятность события В при условии, что событие А уже наступило, по определению, равна

Р_А (В)=Р(АВ)/Р(А) (Р(А)>0).

Дата добавления: 2014-01-07