Метод наименьших квадратов

Если есть основания предполагать, что исследуемая зависимость двух величин Y и X является линейной, то есть удовлетворяет формуле

, (4.5)

и экспериментальный график зависимости y (x) это подтверждает, то есть через доверительные интервалы всех экспериментальных точек можно провести прямую линию, то по результатам измерения величин Y и X, то есть по значениям координат экспериментальных точек, можно определить параметры линейной зависимости k и b. Это можно сделать, по крайней мере, двумя способами.

Первый способ – графический.

· Надо провести прямую линию на графике так, чтобы она пересекла доверительные интервалы всех точек и при этом как можно ближе прошла ко всем точкам. После этого можно приступить к определению k и b.

· k представляет собой угловой коэффициент прямой, поэтому его можно найти как отношение приращения функции D y к приращению аргумента D x. В качестве D x удобнее всего выбрать разность координат крайних точек графика (x _n – x ₁). При этом D y = y (x _n) – y (x ₁).

Рис.4.5. Графический способ определения параметров прямой линии

Обратите внимание: y (x ₁) и y (x _n) – это не ординаты экспериментальных точек y ₁ и y _n, физической величины Y, которые получены до построения графика зависимости y (x). Это значения линейной функции y (x), которую изображает проведённая на графике прямая.

· b – это отрезок, который прямая линия графика отсекает на оси ординат (на вертикальной оси), поэтому для нахождения b надо довести экспериментальную прямую до оси ординат и определить ординату их точки пересечения. Но это правило справедливо только в том случае, когда координатные оси пересекаются в начале координат, то есть в точке с координатами (0; 0). Если же удобнее выбрать другую точку пересечения осей, как это сделано при построении графика на рис.4.5, то нужно использовать другое правило: надо выбрать две точки на прямой, например, точки с координатами (x ₁; y (x ₁)) и (x _n; y (x _n)) и записать уравнение прямой, проходящей через эти точки:

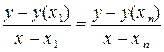. (4.6)

Приведение этого уравнение к виду (4.5) даёт следующее выражение для b:

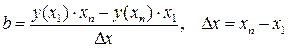. (4.7)

Описанный метод определения параметров прямой линии k и b есть метод их косвенного измерения. А так как всякое измерение обладает погрешностью, то возникает вопрос: как оценить погрешности D(k) и D(b)? Проще всего это сделать так.

· Надо провести через доверительные интервалы ещё две прямые линии: для первой из них параметры k и b должны быть максимально возможными, поэтому её надо провести как можно круче и выше, для второй – значения k и b должны быть минимально возможными, её надо провести как можно полого и ниже.

· После этого погрешности D(k) и D(b) можно определить очевидным образом:

(4.8)

Второй способ определения параметров линейной зависимости, полученной экспериментальным путём, – аналитический.

Он называется методом наименьших квадратов. Его идея в том, что среди всевозможных комплектов пары чисел k и b существует такой единственный комплект, для которого сумма квадратов отклонений ординат экспериментальных точек от соответствующих ординат прямой линии с параметрами k и b, минимальна. Не рассматривая этот метод в деталях, приведём конечные выражения, позволяющие определить k и b.

(4.9)

где обозначено:

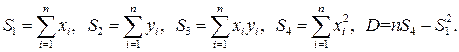(4.10)

В этих формулах n – число экспериментальных точек, а наборы чисел (x _i) и (y _i) – результаты измерений, то есть абсциссы и ординаты экспериментальных точек.

Проделав вычисления по формулам (4.9) – (4.10), следует сделать проверку. Для этого надо по формуле (4.5) вычислить значения ординат прямой линии при двух произвольных значениях x, например при x ₁ и при x _n, затем нанести на график две контрольные точки, то есть точки с координатами (x ₁, y (x ₁)) и (x _n, y (x _n)), и соединить их прямой линией. Если все вычисления проделаны верно, то прямая автоматически пройдёт оптимальным образом, то есть пересечёт доверительные интервалы всех экспериментальных точек и при этом будет максимально приближена к экспериментальным точкам.

Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:

(4.11)

где

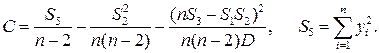(4.12)

Литература

1. Зайдель А.Н. Погрешности измерений физических величин. -Л.: Наука, 1985. – 110 с.

2. Рабинович С.Г. Погрешности измерений. Л.: Энергия, 1978. -258 с.

3. Кунце Х.-И. Методы физических измерений. – М: Мир, 1989. – 216 с.

4. Чернов И.П., Ларионов В.В., Веретельник В.И. Физический практикум. Часть 1. Механика. Молекулярная физика. Термодинамика: Учебное пособие для технических университетов. – Томск: Изд – во Том. Ун – та, 2004. – 182 с.

5. Рипп А.Г. Обработка результатов эксперимента. – Томск: Из – во ТУСУР, 2007, - 60 с.

[1] Это справедливо для нормального закона распределения случайной величины (см. постулаты), но может быть не оправдано для других статистических распределений.

[2] Вопрос о сложении приборных (систематических) и случайных погрешностей актуален только тогда, когда одна из них не более чем в несколько (обычно в 2 – 3) раз превышает другую. В противном случае в качестве оценки погрешности измерения следует указывать только бόльшую погрешность.

[3] Правила округления погрешностей измерения и среднего значения измеренной величины обсудим позже.

[4] Как во всяком правиле, так и в этом - существуют исключения. Это связано с принадлежностью к определенной физической школе. В некоторых лабораториях принято считать все указанные цифры приближенного числа – истинными, а сомневаться начинают в следующей – ненаписанной. Величину погрешности определяют как половину величины ненаписанного разряда, например: ускорение = (9,80 ±0,05) м/с². В нашей лаборатории величина погрешности определяется с «запасом».

[5] Достижимо ли это в принципе? См. естественно – физические пределы точности измерений.

[6] Как во всяком правиле, так и в этом - существуют исключения. См., например, таблицу точных физических констант.

[7] Потеряв сто рублей, о рубле не плачем.

[8]Как минимум, это – правило хорошего тона.

[9] Точнее, закон Ома для участка цепи.

[10] К сожалению, упрощение при этом достигается ценой уменьшения наглядности

Дата добавления: 2014-01-07