Электрическое поле двух равномерно и разноименно заряженных параллельных осей

Электродная система из двух равномерно и разноименно заряженных параллельных осей имеет следующие элементы симметрии:

а) плоскость зеркального отражения, содержащую заряженные оси;

б) плоскость инверсного отражения, перпендикулярную плоскости а) и находящуюся на равном расстоянии от осей;

в) трансляционную симметрию параллельно оси пересечения плоскостей а) и б) с бесконечно малым шагом трансляции.

Плоскость инверсного отражения отличается от плоскости зеркального отражения тем, что при отражении направления векторов и знаков зарядов меняются на противоположные. При таком наборе элементов симметрии для расчета параметров электрического поля в пространстве достаточно определить параметры поля в плоскости, перпендикулярной (нормальной) заряженным осям. Эта плоскость, в свою очередь, может быть разбита на четыре эквивалентные части линиями пересечения с плоскостями зеркального отражения (ось х) и инверсного отражения (ось у). Электрическое поле в этой плоскости представлено на рис.2.11. Поместим начало координат в точку пересечения трех плоскостей и примем потенциал в этой точке равным нулю. Пусть расстояние от начала координат до каждой из осей равно h, линейная плотность заряда осей +t и -t, а расстояния до произвольной точки поля М равны а ₁ и а ₂ соответственно. Тогда, полагая в (2.15) r ₀ = h и r = a ₁, а ₂, имеем

, ,

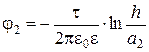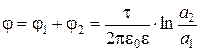(2.45)

Эквипотенциальные линии должны удовлетворять уравнению а ₂/ а ₁ = k, где k – некоторое число. Как упоминалось ранее, это уравнение семейства окружностей. Определим радиусы и центры этих окружностей. Пусть точка

М имеет координаты x, y, z. Тогд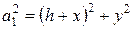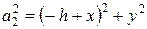а ; , а

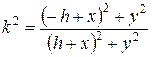. Раскрывая скобки и освобождаясь от знаменателя,

получим: (k ²-1)(x ²+ y ²+ h ²)+2 hx (k ²+1)=0;

x ² +2 hx (k ²+1)/(k ²-1) + h ² + y ²= 0.

Чтобы получить уравнение окружности, нужно полученное уравнение привести к виду (x + x ₀)²+ y ² = R ². Обозначая x ₀ = h (k ²+1)/(k ²-1), добавим (для получения полного квадрата) к левой и правой частям уравнения величину (х ₀)² и перенесем h ² в правую часть:

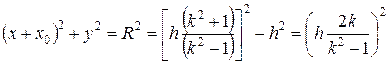
При различных значениях коэффициента k получаются окружности с координатами центра (- х ₀, 0) и радиусом R, где

, (2.46)

(2.47)

При k > 1 - x ₀ < 1 и окружности расположены слева от начала координат. При k < 1 - x ₀ > 1 и окружности расположены справа. Радиус окружности является всегда положительной величиной. Знак в (2.46) следует брать исходя из этого условия, т.е. при k > 1 берется знак плюс, а при k < 1 берется знак минус. Между величинами R, x ₀ и h существует соотношение:

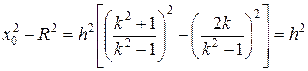(2.48)

Решая квадратное уравнение (2.46) относительно k, получим:

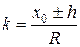(2.49)

Подставляя полученное значение k в (2.45), получим:

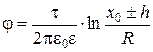(2.50)

Знаки в уравнении (2.50) выбираются так же как и в (2.46), т.е. положительный знак берется для точек, лежащих в левой половине рисунка 2.11 (около положительной оси). Отрицательный знак при h берется для точек, лежащих в правой половине рисунка 2.11 (около отрицательной оси).

Напряженность поля в точке М от каждой из нитей находится по формуле (2.14). Так вектор напряженности и его составляющие вдоль осей х и у от нити +t имеют вид:

;

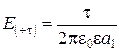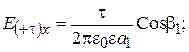
Вектор напряженности и его компоненты от нити -t рассчитываются по аналогичным формулам при замене t на -t и b₁ на b₂. Полный вектор напряженности имеет вид:

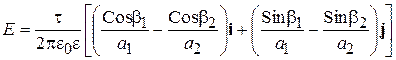(2.51)

Линии поля являются окружностями различного радиуса с центрами, лежащими на оси у. Доказательство этого утверждения приведено в [1.§4.14]. Одна из линий поля совпадает с кратчайшим отрезком между осями.

Дата добавления: 2014-01-07