Поле точечного заряда и проводящего шара

Метод отражения. Поле точечного заряда над бесконечной проводящей плоскостью

Пусть у нас имеется заряд q, находящийся на расстоянии h над проводящей поверхностью. Вследствие кулоновского взаимодействия точечного заряда с поверхностными зарядами произойдет их перераспределение. Равномерное распределение поверхностной плотности зарядов, характерное для уединённой плоскости, превратится в неравномерное распределение со сложной зависимостью плотности зарядов от расстояния между точечным зарядом и позицией на плоскости. Определение параметров поля в произвольной точке пространства по методу суперпозиции с интегрированием по поверхности достаточно сложная и трудоемкая задача. Задача о параметрах поля такой системы зарядов в произвольной точке существенно упрощается, если воспользоваться теоремой о единственности. При анализе поля двух разноименных точечных зарядов (см.§2.10) было показано, что одной из эквипотенциальных поверхностей является плоскость, перпендикулярная прямой, соединяющей заряды. Достаточно положить в уравнении (2.31) координату z=0, как получим эквипотенциальную плоскость ху (001) с потенциалом равным нулю. Если эту эквипотенциальную плоскость заменить тонкой проводящей плоскостью с нулевым потенциалом, то картина поля на рис.2.8б, рис.2.8в не изменится. Как было показано в §1.11, поля выше и ниже такой плоскости не зависят друг от друга. Из этого результата, а также из теоремы о единственности следует метод расчета электростатических полей, который называется метод отражения. Сущность этого метода в приложении к данной системе зарядов состоит в следующем. Сложную систему неравномерно распределенных поверхностных зарядов заменяют одним единственным зарядом–изображением, расположенным под поверхностью на таком расстоянии и с таким зарядом, чтобы картина силовых линий и эквипотенциалей над поверхностью не изменилась. Применяя этот и учитывая решения §2.10, находим, что заряд изображение должен удовлетворять следующим условиям. Он должен быть равен по величине точечному заряду и противоположен ему по знаку. Он должен находиться под плоскостью на продолжении перпендикуляра, опущенного из точечного заряда на плоскость. Расстояние от точечного заряда до плоскости должно быть равно расстоянию от заряда – изображения до плоскости. При выполнении этих условий сложная задача расчета поля параметров поля от заряда, расположенного над заземленной плоскостью сводится к задаче §2.10, а вычисления проводятся по формуле (2.31).

Другим примером применения метода отражения является задача нахождения параметров поля точечного заряда и проводящего шара. Пусть имеется проводящий шар радиуса r и точечный заряд q, находящийся на расстоянии s от центра шара (точка 0). Распределение поверхностной плотности зарядов на шаре не является равномерным. Определение параметров поля в произвольной точке пространства методом суперпозиции представляет собой не простую задачу. Если подобрать заряд – изображение q ¢ таким образом, чтобы картина силовых линий не изменилась, тогда, как и в предыдущем параграфе, задача сведется к нахождению поля от двух точечных зарядов. Система заряд – шар имеет ось симметрии типа С _¥. Из соображений симметрии следует, что заряд – изображение q ¢ должен лежать внутри проводящего шара на этой оси. Пусть проводящий шар заземлен, т.е. его потенциал равен нулю. Поместим заряд – изображение q ¢ на некотором расстоянии х от центра, как показано на рис.2.12. Обозначим расстояния от точечного заряда q и заряда изображения q ¢ до некоторой произвольной точки М на поверхности шара символами а ₁ и а ₂ соответственно. В этой точке, как и в любой другой на поверхности шара должно выполняться соотношение:

,

из которого следует:

.

Как отмечалось в предыдущих параграфах, геометрическое место точек, для которых отношение расстояний до двух заданных точек постоянно, называется на плоскости окружностью, а в пространстве сферой. Из полученного соотношения следует, что для сферической поверхности действительно можно подобрать заряд-изображение. Определим его величину и расстояние от него до центра сферы. Выберем две точки пересечения поверхности шара с осью симметрии 1 и 2. Для точки 1 расстояние а ₁ = s – r, а расстояние а ₂ = r – x. Для точки 2 расстояние а ₁ = s + r, а расстояние а ₂ = r + x. Поскольку

, то 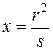, (2.52)

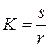, (2.53)

Разберем три возможных варианта изолированной от земли сферы: 1) сфера не заряжена; 2) сфера имеет заряд; 3) сфера имеет потенциал не равный нулю. Во всех трех случаях в дополнение к заряду-изображению q ¢ следует добавить в центр сферы дополнительный точечный заряд q ¢¢. По принципу суперпозиции сфера останется эквипотенциальной, изменится только величина потенциала.

1. Пусть незаряженная сфера изолирована от земли. До того как к ней был поднесен точечный заряд q, суммарный заряд сферы был равен нулю. Поскольку сфера изолирована, то после перераспределения зарядов по поверхности сферы суммарный заряд также останется равным нулю. Дополнительный заряд q ¢¢, который следует разместить в центре сферы, должен быть равен по величине и противоположен по знаку заряду–изображению q ¢¢ =- q ¢, чтобы их сумма была равна нулю.

2. Если на изолированной сфере находился заряд Q, то величина дополнительного заряда должна быть такой, чтобы в сумме с зарядом–изображением получался заряд Q, т.е. q ¢¢ = Q - q ¢= Q + q×r / s.

3. Если сфера была заряжена до потенциала j, то величина дополнительного заряда в центре сферы будет определять потенциал на поверхности сферы, который определится выражением:

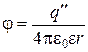(2.54)

Во всех трех рассмотренных случаях потенциал и напряженность в произвольной точке поля определяются суперпозицией трех зарядов q, q ¢ и q ¢¢, а не двух, как было в случае заземленной сферы.

Следует отметить, что в литературе существуют решения задачи электростатики по нахождению положения и величины заряда – изображения для заряда, находящегося вблизи гиперболических поверхностей и других поверхностей сложной формы. На первый взгляд кажется удивительным, как вообще удалось рассчитать поля при такой сложной форме поверхности. Можно сказать, что решение этих задач было найдено инверсным методом, т.е. задом наперед. Решается простая задача двух разноименных неравных по величине зарядов. При анализе решения находится какая-либо эквипотенциальная поверхность, например, гиперболической формы. Эта эквипотенциальная поверхность заменяется поверхностью электрода, а заряд внутри поверхности объявляется зарядом–изображением. Задача о нахождении положения и величины заряда–изображения вблизи гиперболической поверхности оказывается решена.

Дата добавления: 2014-01-07