Нормальная форма уравнений в пространстве состояний

Нормальная форма уравнений в пространстве состояний получается из стандартной формы (10.1) посредством преобразования подобия. При этом предполагается, что собственные числа матрицы А различные.

Введем линейное преобразование

X=MQ, (10.32)

где М - модальная матрица матрицы А.

Уравнения (10.1) перепишем

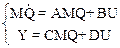. (10.33)

Умножив первое уравнение из (10.33) слева на М^-1, получим

. (10.34)

Так как M - модальная матрица, то

М^-1АМ = L =- диагональная матрица;

где l_i (при i = 1, 2,..., n) - собственные числа матрицы А.

Следовательно, можно записать

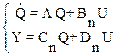, (10.35)

где L=М^-1АМ, В_n= М^-1B, C_n=CM, D_n=D - матрицы;

Q=[q₁,q₂,...,q_n]^T - вектор состояния системы, элементами которого являются новые переменные состояния q_i (при i=1, 2,..., n).

Система (10.35) представляет собой нормальную форму уравнений описания систем управления в пространстве состояний.

Нормальная форма уравнений состояния позволяет декомпозировать многосвязную систему n-го порядка на n взаимонесвязанных систем, при этом дифференциальные уравнения становятся развязанными относительно переменных состояния q₁,q₂,...,q_n, т.е. они имеют вид

, (10.36)

где f_i - внешнее воздействие на i-ю переменную состояния.

Таким образом, переход к нормальной форме существенно упрощает исследование многосвязных систем.

В случае кратных собственных чисел матрицы A диагональная матрица L заменяется матрицей J, которая строится из клеток Жордана, например,

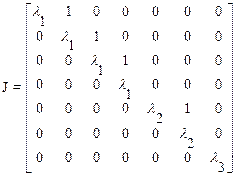. (10.37)

Таким образом, из сравнения уравнений (10.1) и (10.35) следует, что при математическом описании одного и того же динамического процесса различному выбору переменных состояния соответствуют различные матрицы системы, управления, наблюдения, связи и различные векторные дифференциальные уравнения, каждое из которых полностью определяет выходную величину системы.

Пример. Написать уравнения состояний в нормальной форме для динамической системы, представленной на рис.10.3.

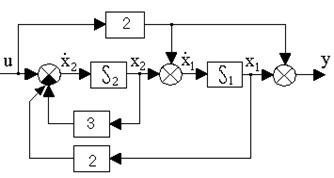
Рис. 10.3. Структурная схема системы в переменных состояния

Решение. Выберем в качестве переменных состояния системы сигналы на выходах интеграторов x₁ и x₂. В этом случае структурной схеме (рис.10.3) соответствует следующая система уравнений (стан-дартная форма)

Откуда матрицы

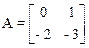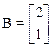, , , D=[2].

Собственные числа матрицы A: l₁= -1, l₂= -2.

Модальная матрица M= и M^-1=.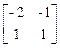

Тогда диагональная матрица системы, матрица управления, матрица наблюдения и матрица связи будут

L=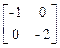, В_n= М^-1B=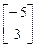, C_n=CM=[-1 -1], D_n=D=[2].

Отсюда получаем уравнения состояний системы в нормальной форме

,

которым соответствует структурная схема системы, приведенная на рис.10.4.

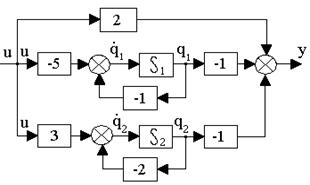
Рис. 10.4. Структурная схема системы в переменных состояния

по полюсам

Дата добавления: 2014-01-07