Механическая система. Моменты инерции

10.2.1. Совокупность материальных точек называется механической системой (МС).

Сила, действующая на материальную точку МС со стороны другой МС, называется внешней силой.

Сила, действующая на материальную точку МС со стороны материальной точки той же МС, называется внутренней силой.

Центр масс механической системы – геометрическая точка, удовлетворяющая условию: сумма произведений масс всех материальных точек, образующих механическую систему, и их радиусов – векторов, проведенных из этой точки, равна нулю.

10.2.2. Моментом инерции механической системы относительно оси 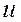или осевым моментом инерции, называется величина, равная сумме произведений масс 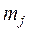всех материальных точек, образующих данную МС и квадратов расстояний 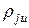от них до данной оси.

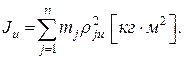
Радиус инерции системы

.

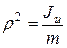10.2.3. Теорема Штайнера (Гюйгенса – Эйлера).

Момент инерции механической системы относительно заданной оси равен моменту инерции этой системы относительно параллельной оси, проходящей через ее центр масс, плюс произведение массы системы и квадрата расстояния между этими осями.

.

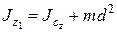10.2.4. Определение моментов инерции.

Для тонкого стержня длиной 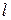с центром 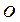по середине

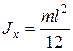(ось 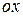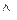оси стержня).

Для тонкого стержня (такого же)

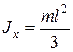(ось 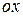на конце стержня).

Дата добавления: 2014-01-07